What is the current consensus on a well-behaving 'Quantum Phase Operator' (in Fock-state basis)?

Question

I'm interested in a quantum operator that returns the phase of some quantized light in the Fock state basis.

That is, if I perform (in a density matrix picture) the expected value of this 'phase operator': $\langle \phi \rangle = \mathrm{Tr}(\rho \phi)= \sum_{nm} \rho_{nm} \phi_{mn}$, I obtain the 'phase' of the light.

In particular, if I give this operator a coherent state $\alpha = |\alpha|e^{i \theta}$ that $\langle \phi \rangle_\alpha = \mathrm{Tr}(\rho_\alpha \phi) = \theta$.

It seems as though there's been a lot of internal debate in the 90's (Although, I have vaguely heard, nowadays, that this is a fairly resolved question.) I have found two operators for phase in the Fock state basis: the Susskind-Glogower operator and the Pegg-Barnett operator. I've attempted to calculate the phase of a coherent state using these operators.

(Note, I'm aware that for a perfect coherent state it's much easier to calculate the phase; you can simply grab the imaginary log of the coherence term between $|0\rangle$ and $|1\rangle$. I am simply using the phase of a coherent state as a test for the phase operator, since the phase is very well defined for a coherent state.)

My attempt at calculating the phase using the Susskind-Glogower operator:

The Susskind-Glogower operator is not unitary, and therefore $\langle \phi \rangle$ is undefined. To remedy this, other operators related to this operator can be calculated, such as $\cos(\phi)$:

\begin{align} (N+I)^{-\frac{1}{2}} a + a^{\dagger}(N+I)^{-\frac{1}{2}} =(a^\dagger a+I)^{-\frac{1}{2}} a + a^{\dagger}(a^\dagger a+I)^{-\frac{1}{2}} \end{align}

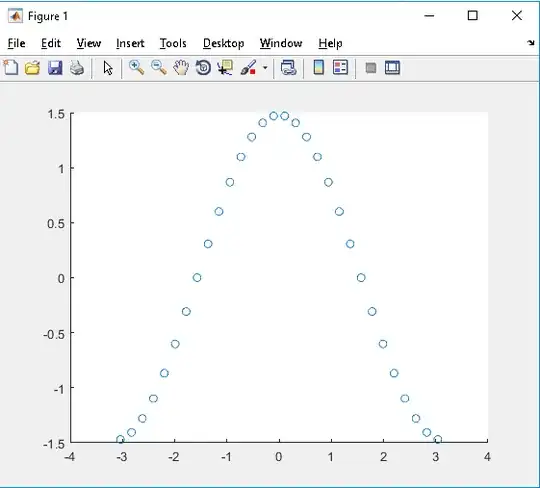
But when I try to calculate value for a coherent state, I get results I do not expect. (Which I posted the code for at the end, if anyone is interested.) I've posted a plot for illustrating this (in which I graph the obtained output phase $\langle \phi \rangle$ as I very the input phase $\theta$ for the coherent state $\alpha = |\alpha|e^{i \theta}.$

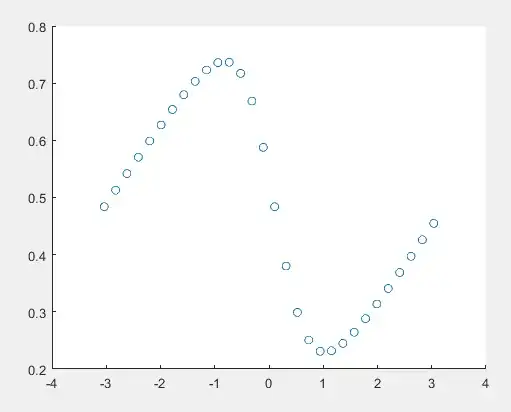
The output corresponds to the operator for $\langle \cos(\phi) \rangle$, and it varies from $-\pi/2$ to $\pi/2$. Shouldn't this vary from $0$ to $1$ since it is the cosine of the argument? And either way, what use is it to find the cosine of the phase?

My attempt at calculating the phase using the Pegg-Barnett operator:

The Pegg-Barnett operator has been said to resolve the nonunitary issues of the Susskind-Glogower operator. The paper I'm using as a reference doesn't appear to explicitly write the operator in the Fock state basis, although they write what a Fock state is in this phase-operator basis:

$$|n\rangle = U|\phi(n)\rangle = \sum_m \exp(in(\theta + 2m\pi)/(s+1))$$

And thus I can write the phase operator as: $|\phi(n)\rangle \langle \phi(n)| = U^\dagger |n \rangle \langle n| U$ . But when I calculate the expected value of the phase $\langle \phi \rangle$ for coherent states, I get incorrect answers (that also vary as I change the value of $|\alpha|$. Here's a visual of how $\langle \phi \rangle$ varies as I change the input phase of $\alpha = |\alpha|e^{i \theta}$:

Here is the Matlab code I used if anyone is interested in going through it (Note: I just recently added a 3rd part that corrects for an error I made in the Pegg-Barnett method):

    % the following script calculates (the cosine of) the phase of the Susskind operator of an input that is a perfect coherent state
    % this output phase is plotted as the input phase is varied 

        N = 30; 
        a = diag(sqrt(1:N),1);
        at = diag(sqrt(1:N),-1);
        iden = diag(ones(1, N+1));
        perf_p = CoherentStateDensityMatrix(0+pi, 3, 30);
        phaseOP = sqrtm(inv(at*a+iden))*a+at*sqrtm(inv(at*a+iden));
        close all
        phaseout = zeros(5, 1);
        phasein = zeros(5, 1);
        totaln = 30;
        for ii=1:totaln        
            phasein(ii) = 2*ii*pi/totaln+pi/2;
            perf_p = CoherentStateDensityMatrix(phasein(ii), 3, 30);
            phaseOP = 1/(2)*((at*a+iden)^(-1/2))*a+at*(at*a+iden)^(-1/2);
            phaseout(ii) = trace(perf_p*phaseOP);
        end
       scatter(wrapToPi(phasein), phaseout)


 % the following script calculates the phase of the Pegg-barnett operator of an input that is a perfect coherent state
 % this output phase is plotted as the input phase is varied    


        s = 30;
        theta0 = 0;
        Umat = zeros(s+1,s+1);
        for nnn = 0:s
           Umat(nnn+1,:) =  1/(s+1)*exp(1i*nnn*(theta0+2*(0:s)*pi/s+1));
        end
        phaseOP2= ctranspose(Umat)*diag(0:s)*Umat;
        perf_p = CoherentStateDensityMatrix(0+pi, 3, 30);

        %I'm assuming this matrix is unitary, consider switching with
        %normal inverse if bugs. 

        for ii=1:totaln        
            phasein(ii) = 2*ii*pi/totaln+pi/2;
            perf_p = CoherentStateDensityMatrix(phasein(ii), 1, 30);
            phaseout(ii) = trace(perf_p*phaseOP2);
        end
        figure
       scatter(wrapToPi(phasein), abs(phaseout))

 %% Second Attempt at Pegg-barnet
 %using: https://arxiv.org/pdf/hep-th/9304036.pdf
 % the following script calculates the phase of the Pegg-barnett operator of an input that is a perfect coherent state
 % this output phase is plotted as the input phase is varied    


        s = 30;
        theta0 = 0;
        rho_n = zeros(s+1, s+1, s+1);
        rho_total = zeros(s+1, s+1);
        for nnn = 0:s
           eig_theta =  theta0+2*(nnn)*pi/s+1;
           theta_n =  1/(s+1)*exp(1i*nnn*(theta0+2*(0:s)*pi/s+1));
           rho_n(:, :, nnn+1) = ctranspose(theta_n)*theta_n*eig_theta;
           rho_total(:,:) = rho_total(:,:)+ rho_n(:, :, nnn+1); 
        end

        perf_p = CoherentStateDensityMatrix(0+pi, 3, 30);

        %I'm assuming this matrix is unitary, consider switching with
        %normal inverse if bugs. 

        for ii=1:totaln        
            phasein(ii) = 2*ii*pi/totaln+pi/2;
            perf_p = CoherentStateDensityMatrix(phasein(ii), 1, 30);
            phaseout(ii) = trace(perf_p*rho_total);
        end
        figure
       scatter(wrapToPi(phasein), abs(phaseout))      







function densitymatrix = CoherentStateDensityMatrix(theta, alpha, maxfock)

rows = 0:maxfock;
a = alpha;
single_row = exp(-a^2/2)*a.^rows./sqrt(factorial(rows)).*exp(1j*theta*rows);
single_column = ctranspose(single_row);
densitymatrix = single_column*single_row; 

end

Answer 1

As I understand the situation, the current consensus is that the best way to measure phase is using a POVM, $$ \int \frac{\mathrm d\phi}{2\pi}|\phi⟩⟨\phi| = 1 \quad\text{where}\quad |\phi⟩ = \sum_{n=0}^\infty e^{in\phi}|n⟩, $$ and that it's not particularly worth it to go looking for an explicit operator.

Using this convention, if you want the phase distribution for a coherent state $|\alpha⟩$, you just plot $$ f(\phi) = |⟨\phi|\alpha⟩|^2 $$ which looks like this for $\alpha = r e^{i\theta}$ with $\theta=0$ and $r=0.5$, $1$, $2$ and $5$ (in blue, yellow, green and red, resp.):

As you'd expect, the higher the mean photon number, the smaller the phase uncertainty.

I'm unable to locate good references for this formalism at the moment. I'll add them later if I do find them.

Answer 2

The Pegg-Barnett operator is in principle a good phase operator if the Fock-space is truncated (which is usually not a problem, to put a wavevector into the computer, you'll need a truncation anyway.)

So, what is the reason that you get this 'wavy'-pattern in your figure instead of a straight line? A first thing to keep in mind is the periodicity of the phase: so the best thing you can hope for is a sharp sawtooth function. In practice, a PB-operator (and basically any other attempt to calculate a phase) must assume an interval e.g. $[0,2\pi[$, implying a sharp cut at the edge. I see you did retrieve the periodicity. The reason your edges are smoothening is the following: A coherent state is not a phase eigenstate, so it has a finite variance of the phase. This becomes an issue when your coherent state is located close to the phase-cut: then part of the state (a tail of the distribution) actually crosses this cut! If you have for example a state $|\alpha\rangle=|0\rangle$, half of the state has a phase $\approx0$ and the other half a phase $\approx2\pi$, giving a total result of $\pi$!

As a practical approach to find a way out, you (as I briefly explained in an an answer to an old question of my own https://physics.stackexchange.com/a/380324/25292) can exploit that the PB-phase has a free parameter (the reference phase, corresponding to where you lay the phase-cut) and update this one dynamically until you get a proper result. Some MATLAB code I used (currently assumes wavefunction instead of density matrix, but the extention is straightforward as I have indicated in the code):

function [phase,Nit,phaseop]=refinedPBphase(psi)
%REFINEDPBPHASE calculate the phase of a wavevector psi (column). Starting point is
%the Pegg-Barnett formalism (see arXiv:hep-th/9304036). Through the
%iterations, it is possible to avoid nasty effects from the phase-cut by
%dynamically adapting the reference phase (as long as the state considered
%is at least somehow localized in phase space). Outputs the phase, numer of 
%iterations used and the final phase operator.

 Wouter V, 2018

Nmax=length(psi); indvec=1:Nmax;
thetazero=-pi; %Initiate reference phase

Tol=0.001; %Criterion when to be satisfied with the result.
updphase=0;
diff=Tol+1;

Nit=0; %Keep track of number of iterations
maxit=100; %maximal amount of iterations
while (diff>Tol)

%construct the phase operator
phaseop=2*pi/Nmax*exp(1i*(indvec.'-indvec)*thetazero)./(exp(2i*pi*(indvec.'- 
indvec)/Nmax)-1); 
phaseop(isinf(phaseop))=thetazero+(Nmax-1)*pi/Nmax;



oldphase=updphase;
updphase=wrapToPi(real(psi'*phaseop*psi)); %updated phase; change to wrapToPi(real(trace(phaseop*rho))) for mixed state

diff=abs(angdiff(updphase,oldphase));
thetazero=updphase-pi; %new reference phase, further away from our state of interest

Nit=Nit+1;

if(Nit>maxit)
warning('refPB:noconv',['refinedPBphase unable to reach tolerance after maxit ',num2str(maxit),' iterations']);
Nit=Inf; %Retrieve failure afterwards
break;
end

end

phase=updphase;

end

I had exactly the same requirement as you: the linear (sawtooth) relation between input and 'measured' phase for a coherent state, and it works perfectly. In practice, I have been applying this mainly to states with a 'banana' shaped W-function, so it should definetely work for your states. Convergence is usually reached without a problem as long as the density is not very close to zero. Of course, the state should not be spread out a full $2\pi$ for it to work (then there wouldn't be any phase anymore). You obtain the suitable operator as a result, which can be further used to calculate higher moments of the phase.

Reference: https://doi.org/10.1103/PhysRevA.100.013804 (Appendix B)

Answer 3

The eigenvalues of self-adjoint linear operator are real numbers. But a phase is not a number but either an angle (as you requested it), which is an infinite set of real numbers differing by an integral multiple of $2\pi$) or (the more standard definition) a complex number of modulus 1. Therefore no self-adjoint linear operator can have the phase as an eigenvalue, and your request is unanswerable. However, sine and cosine of the angle $\theta$ are commuting, self-adjoint operators, with spectrum in $[-1,1]$ and joint eigenvectors, and $P:=\cos\theta+i\sin\theta$ is a normal operator whose spectrum consists of the phases $e^{i\theta}$. This is the closest sensible answer to your question.

For the impossibility of quantizing an angle directly, and for the definition of the sine and cosine operators, see the discussion and references in my answer at Why doesn't the phase operator exist?

Answer 4

This is just a proposal. I have no knowledge whether it has been tried in the literature. (Having said that, I am aware of the phase operators that you are refering to. This proposal is not related to any of that.)

Since what you are interested in is the analogue of the phase of a coherent state, one may use the phase space analogy for coherent states represented in terms of Wigner functions. So, if one can compute the Wigner function $W(q,p)$ for your state, one can determine its centre of mass via the first moments in phase space $$ q_0 = \int W(q,p) q\ dq $$ $$ p_0 = \int W(q,p) p\ dp $$ Then one can construct $$ \alpha = \frac{1}{\sqrt{2}} (q_0+ i p_0) $$ and from that compute the phase.

In my view that would give you the closest representation of the phase of a state that would corresponds to its equivalent for a coherent state. Unfortunately, I don't see a simply way to define a quantum operator that can perform the complete process.