Is there a quantum analogue of Mean Value Theorem theorem?

Question

Background

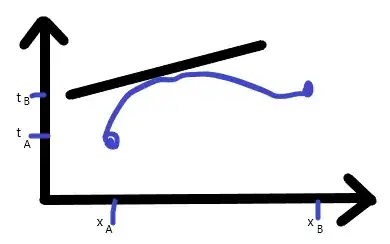
I was thinking of Mean Value Theorem in the context of classical mechanics I have $2$ points $A$ and $B$ and my particle goes from $A$ to $B$ then I know the velocity of the particle at a time $\tilde t$ is given by $\dot x(\tilde t)=\frac{x_a-x_b}{t_a - t_b}$ where $ \tilde t$ is a point between $t_a$ and $t_b$ as shown below:

Question

My question is: is there a quantum analogy of Rolle's theorem for the sum over histories formulation of quantum mechanics? To elaborate further, we know how to define velocity via the Heisenberg picture as: $\hat v = -i [H,x]$ and surely one can make a statement about how Rolle's theorem would apply in the quantum realm which is each path multiplied by a phase factor? If so, what is the mathematical statement?

Edit

Just as Rolle's theorem enabled one to make a statement about the velocity between points $x_A$ and $x_B$. Is there a statement one make about the velocity between the points $x_A$ and $x_B$.

For example consider the amplitude given by:

$$ A = \langle x_A|e^{\frac{iH(t_A - t_B)}{\hbar}}| x_B \rangle$$

Splitting into $N$ parts:

$$ A = \langle x_A|(e^{\frac{iH(\Delta t)}{\hbar}})^N| x_B \rangle$$

Let $\hat v | v \rangle = v | v \rangle$ where $v$ is the velocity operator. Then, inserting the fat identity:

$$ A = \langle x_A| (e^{\frac{iH(\Delta t)}{\hbar}}) \Big( \int dv_{N-1} | v_{N-1} \rangle \langle v_{N-1} \Big| ) (e^{\frac{iH(\Delta t)}{\hbar}}) \dots(e^{\frac{iH(\Delta t)}{\hbar}}) \Big( \int dv_{1} | v_{1} \rangle \langle v_{1} \Big ) (e^{\frac{iH(\Delta t)}{\hbar}}) | x_B \rangle$$

Rather than re-derive the whole sum over histories with the velocity operator. We assume the Hamiltonian is a linear function of position and velocity. You mean that it is the sum of a function of position and a function of velocity.. Let, $\hat H$. Let them be $\hat T(\hat v)$ and $\hat V(\hat x)$

$$ A = \langle x_A| (e^{\frac{i(T+ V)(\Delta t)}{\hbar}}) \Big( \int dv_{N-1} | v_{N-1} \rangle \langle v_{N-1} |\Big ) (e^{\frac{i(T+ V)(\Delta t)}{\hbar}}) \dots(e^{\frac{i(T+ V)(\Delta t)}{\hbar}}) \Big( \int dv_{1} | v_{1} \rangle \langle v_{1} \Big ) (e^{\frac{i(T+ V)(\Delta t)}{\hbar}}) | x_B \rangle$$

Now I conjecture it each path the $e^{\hat T}$ acting on $|v \rangle$ will get $\frac{x_a-x_b}{t_a - t_b}$ at least once in the limit $N \to \infty$.

How do I make the last line more precise?

Answer 1

1. There is no velocity in the Hamiltonian formalism. If you're using a Hamiltonian, you must use momentum, not velocity. See this question and my answer for why the Hamiltonian is a function of position and momentum, but not velocity.

2. The momentum operator is proportional to the time derivative of the position operator (in the Heisenberg picture) only on-shell, but the paths in the path integral are not on-shell, i.e. not necessarily solutions to the equations of motion, and we are using time-dependent states, i.e. the Schrödinger picture, in the derivation anyway.

Therefore, the $\lvert v\rangle$ in your question do not exist. You can do a similar derivation involving momentum, but it is an off-shell derivation where momentum and position are a priori unrelated. This is, in some sense, fortunate, because the paths in the path integral formalism after taking the limit are almost always not differentiable - the mathematically rigorous measure on the space of paths is a conditional Wiener measure, under which the differentiable paths have zero measure - therefore you cannot apply Rolle's theorem to a generic path anyway.