In a metric, such as
$$ d\tau^2=g_{11}dt^2-g_{22}dr^2 $$
the longest interval $d\tau$ between two events obviously is when $dr=0$ simply due to the sign. This is the rest frame with no motion in space and consequently no time dilation due to motion. Any $dr\ne 0$ would result in a motion with a stronger time dilation and therefore decrease the interval or the proper time.
The radial geometrized Schwarzschild metric inside the event horizon is
$$ d\tau^2 = \left(\frac{r_s}{r}-1\right)^{-1} \,dr^2 - \left(\frac{r_s}{r}-1 \right)\,dt^2\tag{1} $$
Where $r$ is the coordinate time and $t$ is a spatial coordinate orthogonal to time and therefore not pointing to the center. As mentioned above, the longest proper time is when $dt=0 $ and therefore
$$ d\tau^2 = \left(\frac{r_s}{r}-1\right)^{-1} \,dr^2 $$
Or
$$ d\tau =\dfrac{dr}{\sqrt{\dfrac{r_s}{r}-1}} $$
Solving
$$ \tau=-r\sqrt{\dfrac{r_s}{r}-1}-r_s\arctan\left(\sqrt{\dfrac{r_s}{r}-1}\right)+C $$
From $\,r=r_s\,$ to $\,r=0\,$ the longest possible lifetime inside the black hole is
$$ \tau=\dfrac{\pi}{2}r_s=\pi M $$
More rigorously, the bound solution of the geodesic equations for the radial metric $(1)$ yields the following geodesics (where $R$ is the radius, from which the fall starts at rest)
$$ \tau=\dfrac{R}{2}\sqrt{\dfrac{R}{2M}}\left(\arccos\left(\dfrac{2r}{R}-1\right)+\sin\left(\arccos\left(\dfrac{2r}{R}-1\right)\right)\right) $$
And
$$ t=\sqrt{\dfrac{R}{2M}-1}\cdot\left(\left(\dfrac{R}{2}+2M\right)\cdot\arccos\left(\dfrac{2r}{R}-1\right)+\dfrac{R}{2}\sin\left(\arccos\left(\dfrac{2r}{R}-1\right)\right)\right)+ $$
$$ +\, 2M\ln\left(\left|\dfrac{\sqrt{\dfrac{R}{2M}-1}+\tan\left(\dfrac{1}{2}\arccos\left(\dfrac{2r}{R}-1\right)\right)}{\sqrt{\dfrac{R}{2M}-1}-\tan\left(\dfrac{1}{2}\arccos\left(\dfrac{2r}{R}-1\right)\right)}\right|\right) $$
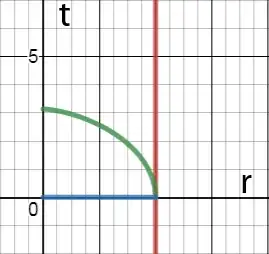
Plotting these functions for the fall from the horizon $r=2M$ confirms no spatial movement $t=0$ (blue line), as well as the maximum proper time $\tau=\pi M$ (green line). Please note that time $r$ on the chart moves from right to left.
In comparison, the next plot represents a fall from $r=5M$ showing time $t$ above the horizon diverging to infinity and showing a fast spatial movement along $t$ inside the horizon causing a stronger time dilation that results in a (roughly twice) smaller value of the proper time $\tau$ between the horizon at $r=2M$ and the singularity at $r=0$.
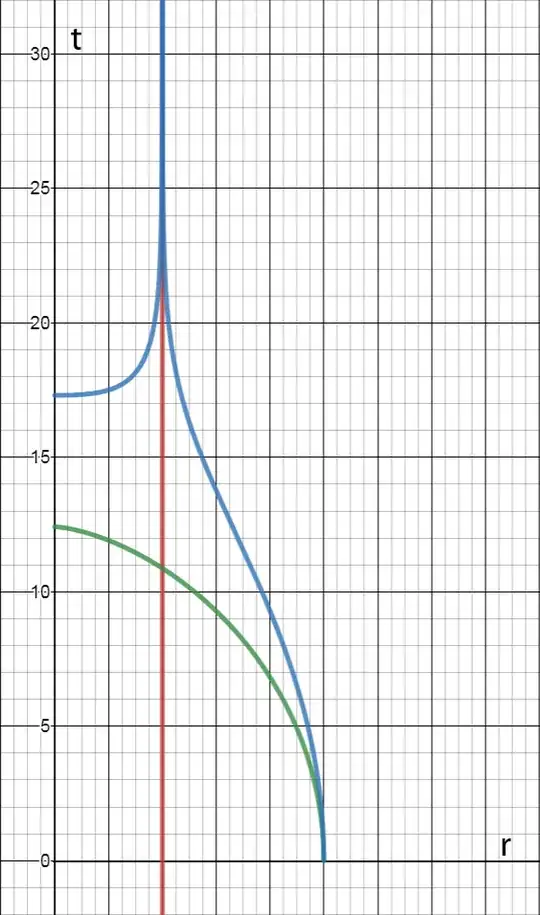
The charts show that gravity inside a black hole causes a deceleration of moving bodies $\dfrac{d^2t}{dr^2}\lt 0$ and does not accelerate bodies at rest with the speed of $\dfrac{dt}{dr}=0$.
Using these results, we can now visualize the geometry of a Schwarzschild black hole in a spacetime reduced by one dimension
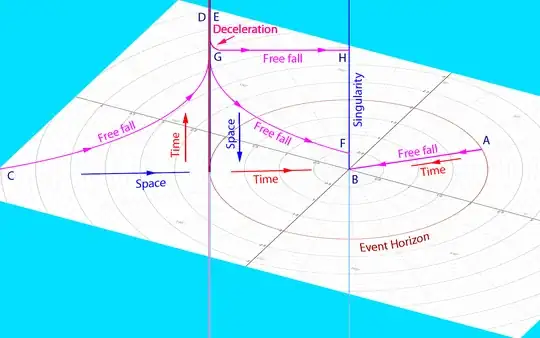
In this diagram, the coordinate $t$ is vertical. Outside the event horizon $t$ represents time; inside the event horizon $t$ represents a spatial dimension that does not point to the singularity. The radial coordinate $r$ is spatial outside the horizon, but represents time inside. Thus the singularity is a line along the spatial dimension of $t$ at the time of $r=0$.
A body falling from the event horizon $A$ has no momentum along the spatial dimension of $t$. Therefore this body is stationary inside and moves only in time along $r$ from $A$ to $B$. Due to the symmetry considerations, this body cannot gain a momentum along the spatial direction of $t$ during the fall. For this reason, a body falling from the event horizon would have the longest possible lifetime inside the horizon, as discussed above. While we call this movement "a free fall", in fact the body remains stationary in space.
A different body in a free fall from infinity or from any point outside would move outside the horizon along the geodesic from $C$ to $D$. Passed the point $D$ time diverges to infinity for an external observer. After crossing the horizon, this body continues moving along the geodesic from $E$ to $F$ (see also the geodesic chart above). Because this body moves in space along the dimension of $t$, the body experiences a time dilation due to motion that shortens its total proper time inside the black hole.
To extend the proper time, the movement along $t$ must be decelerated and stopped, as shown at $G$. After that the body is stationary with no movement in space along $t$ while moving only in time along $r$ from $G$ to $H$. Obviously, provided the deceleration time is negligible, the lifetime of this body is maximized as discussed earlier.


