The answer to your question lies in the fact that you are dealing with two different electric fields which are competing with one another and that the non-conservative electric field produced by the inductor owes its existence to a changing magnetic flux produced by a changing current in the circuit.
One electric field produced by the voltage source is trying to change the current and the other electric field produced by the inductor is trying to stop the change in current but the change in current has to happen because if it didn't the electric field produced by the inductor would cease to exist.
The definition of self-inductance $L$ is $L=\frac {\Phi}{I}$ where $\Phi$ is the magnetic flux and $I$ is the current.
Differentiating the defining equation with respect to time and then rearranging the equation gives $\frac{d\Phi}{dt} = L\frac{dI}{dt} \Rightarrow \mathcal E_{\rm L} = - L\frac{dI}{dt} $ after applying Farday's law where $\mathcal E_{\rm L}$ is the induced emf which is going to try and prevent any change in the current.
Consider a series circuit which consists of an alternating voltage source and an ideal inductor.
The alternating voltage source is trying to change the current in the circuit by varying the electric field in the circuit.
The inductor is trying to oppose any change to the current and hence the magnetic flux by producing a non-conservative electric field in opposition to the field produced by the voltage source.
The strength of the non-conservative field which will oppose the electric field trying to change the current in the circuit is determined by the rate of change of current in the circuit.
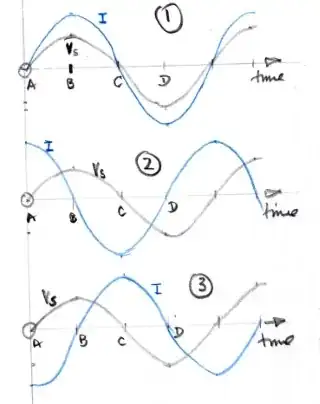
Suppose the current and the supply voltage are in phase with another as in graph 1.
Just after time A the electric field due to the supply voltage is increasing which leads to an increase in the current in the circuit.
The inductor needs to generate an electric field which tries to negate small electric field produced by the voltage source.
However, at this time the rate of change of current is a maximum.
At time B the electric field produced by the voltage source is large and to negate its effect the inductor must produce a large electric field in the opposite direction yet at this time the rate of change of current is near zero.
Suppose that the current leads the supply voltage by $90^\circ$ as in graph 2.
Just after time A the electric field due to the supply voltage is increasing which leads to an increase in the current in the circuit.
The inductor needs to generate an electric field which tries to negate small electric field produced by the voltage source.
The good news is that at this time the rate of change of current very small, but the electric field produced by the inductor would be in the same direction as the electric field produced by the voltage source.
At time B there is a large rate of change of current so that the inductor would produce a large electric field to negate the electric field produced by the voltage but again that field is in the wrong direction.
You could go on like this until you get to graph 3 where the supply voltage leads the current by $90^\circ$ and you will find that at all times the magnitude of the electric field produced by the inductor mirrors that produced by the voltage source but is opposite in direction.
In terms of energy the graphs of supply voltage, current and power produced by the voltage source look like this. if the phase difference if $90^\circ$.
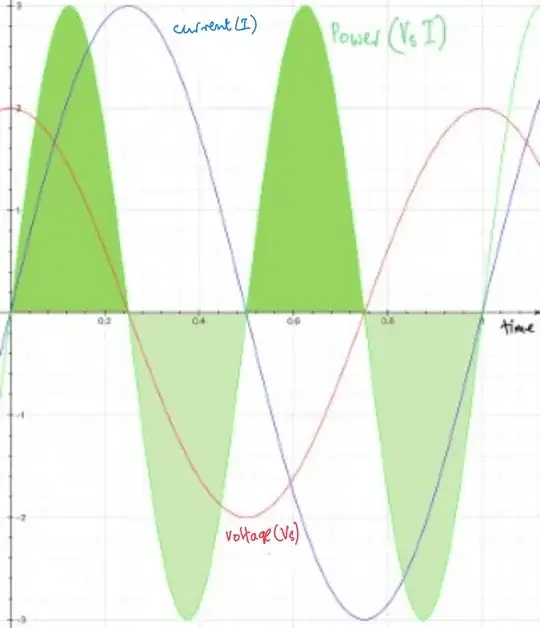
The darker green areas represent energy flowing from the voltage source to the inductor and the lighter green areas represent energy floring from the inductor to the voltage source.
A corresponding power graph for the inductor would be the mirror image of the one for the voltage source.
Overall the important thing to realise is that even if two emf in a circuit look as though they negate each other there can still be a transfer of energy between the two sources of emf.

