If induced voltage (back-emf) is equal and opposite to applied voltage, what drives the current?

Question

Suppose we have a circuit with a voltage source, a switch open and an inductor all in series. If we close the switch, the potential difference of the voltage source is instantaneously applied to the inductor. As the current starts to build up, induced voltage from the inductance opposes it. If the induced voltage (back-emf) is equal and opposite to the applied voltage, and the net voltage is zero, what drives the current then? All I could find on the web was this:

"...it is difficult to realise that there can be a current without a 'resultant' emf. Faraday's law states $e = LdI/dt$ and if there is no resistance $e = E$. It is the electrical analogy of constant velocity with no need for a resultant force. If there is resistance then $e = LdI/dt = E - Ir$ ... 'resultant' $\text{emf} = e$"

Could you expand a little bit more on this idea?

Answer 1

The answer to your question lies in the fact that you are dealing with two different types of electric field (conservative and non-conservative) and that the non-conservative electric field owes its existence to a changing magnetic flux produced by a changing current.

The definition of self-inductance is $L=\dfrac {\Phi}{I}$ where $\Phi$ is the magnetic flux and $I$ is the current.

Differentiating the defining equation with respect to time and then rearranging the equation gives $$\dfrac{d\Phi}{dt} = L\dfrac{dI}{dt} \Rightarrow \mathcal E_{\rm L} = - L\dfrac{dI}{dt} $$ after applying Faraday's law where $\mathcal E_{\rm L}$ is the induced emf produced by a changing current.
The electric field associated with the changing magnetic flux is non-conservative.

Consider a circuit consisting of an ideal cell of emf $V{\rm s}$, a switch and an ideal inductor all in series with one another.

At time $t=0$ the switch is closed.
The initial current must be zero which you can understand with an appreciation of the fact that mobile charge carriers have inertia and thus cannot undergo an infinite acceleration.

The conservative field produced by the cell is trying to increase the current from zero but the non-conservative field produced by the inductor is trying to stop the current changing.
Which field wins?
At $t=0$ there is no current so it would appear that it is a draw between the two fields, but the non-conservative field can only stop a current flowing at $t=0$ on condition that the current changes.
So the current has to increase despite the opposition of the non-conservative field and so it continues with the current increasing due to the conservative field despite the opposition of the non-conservative field.
All that the non-conservative field can do is slow down the rate at which the current changes; it can never stop the current changing as then it (the non-conservative field) would no longer exist.

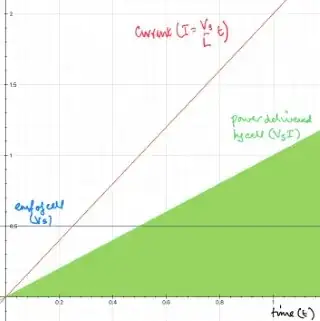
For this example the current $I = \dfrac{V_{\rm s}}{L}\,t$ and the energy delivered by the battery $\dfrac 12 V_{\rm s} I t = \dfrac 12 \dfrac{V_{\rm s}^2t^2}{L}$, is equal to the energy stored in the magnetic field produced by the inductor, $\dfrac 12 L I^2 = \dfrac 12 \dfrac{V_{\rm s}^2t^2}{L}$, and is the area under the power against time graph (shaded green).

Answer 2

If the emf due to the solenoid is assumed to oppose the applied voltage and have equal magnitude (in volts), there is zero net electromotive force intensity in the wire acting on current. Since some current is assumed to be present, this means the current flows even while the net electromotive force (result of both conservative and induced electric force) vanishes.

This is possible for wire made of perfect conductor (superconductor). In practice, there is always some resistance to current so the induced emf along the inductor coils cannot exactly cancel the applied voltage at all times.

Answer 3

In a resistor $I=\frac{V}{R}$. If somehow the current was less, ie a switch was just closed, it would increase until it matched the equation. This is because if the current was less, then the back emf from the resistor would not equal the driving emf and thus current would want to increase. Since in this model there is no inductance, there's nothing to prevent an instantaneous change in current, so the circuit can equilibrate instantly.

Now lets consider the inductor. Before the switch is closed there is no current, no emf, and importantly no change in current. When the switch closes now there is still no current, but there is an applied emf. Let's suppose the change in current tried to remain less than $\frac{V}{L}$. Now the back emf from the inductor would be less than the emf so there would be a net emf to increase the current. So the rate of current increase rises until the back emf of the inductor equals the applied emf. Additionally, since nothing prevents instantaneous changes in rate of change of current, the circuit can equilibrate to steady state (of constantly increasing current) instantly.

Answer 4

(1) A magnetic field is generated when a current passes through a wire. This current can be unchanging. As an example (for now ignore what happens initially and focus on steady state ) wrapping wire around a nail and connecting the ends to a DC source will channel the magnetic field through the nail creating a magnet. The magnetic field is constant and so is the current.

(2) When a magnetic field cuts across a wire it induces an EMF.

If the wire is wrapped in a coil formation, as the current through the wire increases the magnetic field will grow cutting across turns of the coil which will induce an emf in the wire. This induced EMF opposes the applied EMF. You already know that. The key point is a current must flow in the wire because of point 1) above. The inducted back emf and the current it creates is overtaken by the applied current by an infinitesimally small amount as the applied current increases.

Because this current is infinitesimally small you wont see it on a graph of AC voltage vs. current for a purely inductive circuit. Instead the graph will show no current flow as the AC applied voltage goes from 0 to 90 degrees. But between 0 and 90 degrees an infinitesimally small current does flow or you wouldn't have a change in current through the inductor.

When an equation is a derivative $V=L\dfrac{\mathrm d i}{\mathrm d t}$ your looking at a tangent line to the function and picking two points on that line that are infinitesimally close together. When you take the average of those two points you can ignore the infinitesimal space between the points and assume that you have a point at an instant. But the space between the points is real. My point is that any time calculus is involved you can have these mental conflicts and it helps to think about an "infinitesimal change".

Answer 5

Well... When the back emf is equal to the voltage supplied by the battery, it is not really hard or anything counter intuitive to realize how the current exists in such a case. See, all you need to realize is what is actually the back emf? When the charges in motion, tries to pass through an inductor - the inductor converts its kinetic energy into magnetic energy and slows down the moving charges. The actual force which acts on the charges to slow them down is the induced electric field due to changing magnetic field associated with the inductor. Now what is back emf? It is simply the energy taken by the inductor per unit charge. According to the Kirchoff's law (Energy Conservation), a charge particle in motion expenses the same energy in its motion outside the battery as it gains inside the battery. So all the energy that an electron gains in the battery will be transferred to the magnetic energy of the inductor. So, back emf = source voltage. But, obviously, current exists, because, first the charge gets accelerated inside the battery and then it slows down working against the back emf.

Answer 6

The short answer: you're right – they CAN'T be equal, even though every loop law that runs through an inductor assumes it to be the case.

Here's how I think about it: since an inductor's back-EMF is a consequence of Faraday's Law, it's subject to the same negative-feedback condition imposed by Lenz's Law. That is: the back-EMF can't ever meet or exceed the ∆V that would change the current through it.

I conceive of an inductor's role in a circuit as analogous to inertial mass in a block-and-spring system. The mass resists all change to its velocity, positive or negative, but any finite mass can't FULLY reduce a force's dv/dt to zero; to do so would require an infinite mass. Analogously, I think of inductance (L) as current-inertia. Hence, it would take an infinite inductance to produce a back-EMF precisely equal in magnitude to the applied voltage.

(By extension, an "infinite inductor" would perfectly maintain the instantaneous current flowing through it, forever.)

You've hit upon one of the many assumptions of convenience electric circuits make; it's only shrieking about how Kirchhoff is NEVER wrong (spoiler alert: yes, sometimes it is) from here on down.