Are contravariant basis vectors and basis 1-forms identical?

Question

The reason I'm asking this is because I am trying to develop a set of notes from my reading of MTW (and Wrede, Menzel, Bergman, etc.).

I represent covariant basis vectors with $\mathfrak{e}_{i}$, or if they are orthonormal $\hat{\mathfrak{e}}_{i}$. In cases where the author is explicitly using the terminology "contravariant basis vector", I use, $\mathfrak{e}^{i}$ and $\hat{\mathfrak{e}}^{i}$ for the dual entities. My desire to represent basis 1-forms using identical with contravariant basis vectors started as a software issue. I don't have a pretty way to consistently represent bold-faced Greek letters with the editors I use. But it has become a matter of principle.

I believe I can continue to use my contravariant basis notation for the basis 1-forms appearing in MTW with impunity. That is, I won't have to go back and change my notes because it turns out that basis 1-forms and contravariant basis vectors are geometrically distinct entities.

I have no way of concisely summarizing my understanding of these concepts. Every author has a different approach to developing the fundamentals of tensor analysis and differential geometry pertinent to applications in physics.

There are two prima facie different "schools".

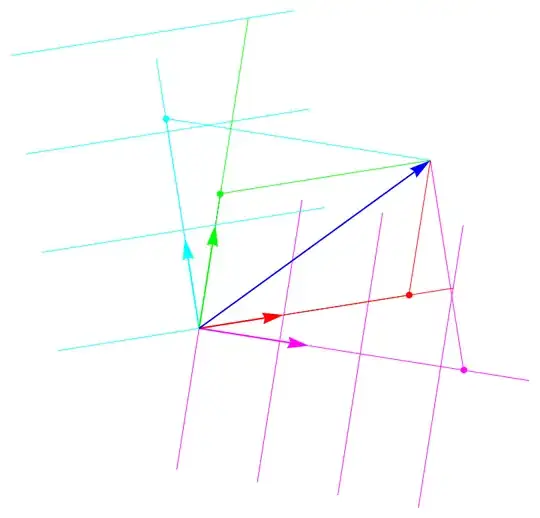
For example, Menzel and Wrede use dual covariant/contravariant basis vector sets. The MTW school uses covariant basis vectors and their dual basis 1-forms. I understand that basis vectors and basis 1-forms are intended to induce conceptually different notions in the student's mind. As I understand these, the (covariant) basis is represented as an arrow because that depicts the distance along one coordinate curve between points of intersection with other coordinate curves. That is, the distance between "lines" of the coordinate mesh.

Basis 1-forms represent the "density" of intersecting coordinate curves. So an arrow representation is misleading. By this reasoning, depicting the gradient with an arrow is misleading because it is actually a 1-form which represents the density of surfaces of constant value. (There is, however, a signed normal direction to each such surface.)

Contravariant basis vectors are typically concocted in some way to support transformation invariance.

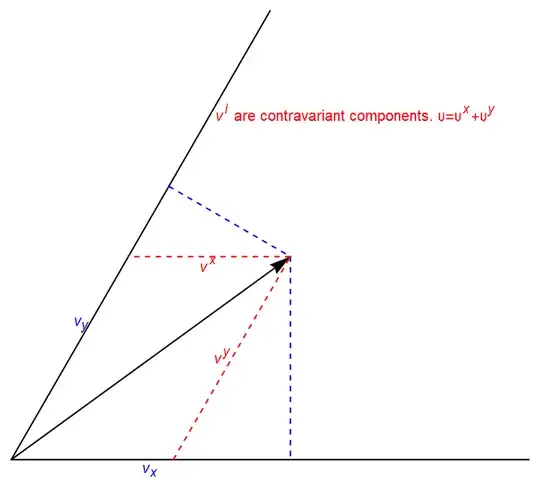
But, to me, basis 1-forms and contravariant basis vectors appear to represent the same commodity with different labeling. For example: if we denote the dual basis 1-forms by $\omega^{j}$, then

$$\mathfrak{e}_{i}\cdot\mathfrak{e}^{j}=\left\langle \mathfrak{e}_{i},\omega^{j}\right\rangle =\delta_{i}^{j} \, .$$

Is this a reasonable assessment? Is there an example situation where identifying basis 1-forms (dual to covariant basis vectors) with contravariant basis vectors (dual to covariant basis vectors) fails?

Answer 1

Is this a reasonable assessment? Is there an example situation where identifying basis 1-forms (dual to covariant basis vectors) with contravariant basis vectors (dual to covariant basis vectors) fails?

No, the reconciliation between the old and "new" concepts must be complete.

The 1-form dx is not the same as the infinitesimal dx, as you know. In this context it is considered not a 'number', but a member of the cotangent space $T_p^*$.

Introducing the 1-form concept removes the problems involved relating to attempting an intuitive understanding of the idea of 'infinitesimally small' changes $dx^i$ in the coordinates $x^i$.

In order to derive the gradient of a function $f(x)$, (as the usual example), the "old" teaching method required the consideration of an infinitesimally small change in $x'$, call it $dx^i$, followed by finding the corresponding 'infinitesimally small' change in $f$, call this $df$ and divide them, to get $ \frac{\partial f}{\partial x^i} $.

This is not a very rigourous setup, requiring "faith in the system", but, as explained by Michael Spivak :

No-one wanted to admit this was nonsense because true results were obtained when these infinitely small quantities were divided into each other (provided one did it in the right way). Eventually it was realised that the closest one can come to describing an infinitely small change is to describe a direction in which this change is supposed to occur, i.e. a tangent vector. Since df is supposed to be the infinitesimal change in f under an infinitesimal change of the point, df must be a function of this change, which means that df must be a fimction on tangent vectors. The $dx^i$ themselves then metamorphosed into functions, and it became clear that they must be distinguished from the tangent vectors $ \frac{\partial f}{\partial x^i} $. Once this realisation came, it was only a matter of making new definitions which preserved the old notation, and waiting for everybody to catch classical notions involving infinitely small quantities became functions on tangent vectors, like $df$, except for quotients of infinitely small quantities, which became tangent vectors, like $df/dt$.

To your point in the comments:

Any distinctions involve notational differences.

It's far more than notational differences, it's a complete conceptional distinction that was developed at the start of the last century. Entities such as exterior derivatives, the generalised version of Stokes Law, and many more concepts are developments arising from going the 1-form route.

Is there not a 1-1 correspondence between basis 1-forms and contravariant basis vectors? Is there any information contained in one which is not contained in the other? I'm at a loss to find an example where I can use a basis 1-form to do something I cannot do with a contravariant basis vector.

Looking at the solutions to GR equations made me appreciate (in every sense of the word) the usefulness of the 1-form treatment, try this yourself:)

.

Answer 2

Are $i$ and $-i$ identical? Are left and right, clockwise and anticlockwise identical?

Duality/symmetry and being identical are two different things. You can tell they are not identical based on how they interact with each other (i.e. an expression involving both of them, much like how the product of $i$ and $-i$ is 1, but the product of $i$ and $i$, or $-i$ and $-i$, are -1, which behaves differently from 1).

Answer 3

Gravitation and Inertia Ignazio Ciufolini & John Archibald Wheeler" pages 416-417. 1-forms and covariant vectors are defined as synonymous. of the transformation law for 1-forms they state ”This is just the coordinate dependent definition of a covariant vector."

The answer is: yes, the basis 1-forms and contravariant basis vectors typically used in physics are identical objects. Any distinctions involve notational differences, particularly in how they are used in binary operations. Most significantly; when the basis 1-forms are written as coordinate differentials $dx^i$ and are used as the projection operators mapping vectors to their individual components, we have the defining characteristic of a basis 1-form:

$$\left\langle dx^{i},\mathfrak{v}\right\rangle =\mathfrak{e}^{i}\cdot\mathfrak{v}=v^{b}\mathfrak{e}_{b}\cdot\mathfrak{e}^{i}=v^{i}$$.

In addition, both types of object transform by the same contravariant transformation law.

---

Edit to add the following references:

Compare Mathematical Physics, by: Donald H. Menzel $\S\S$ 2-31 Tensor Analysis, to Gravitation, by Charles W. Misner, Kip S. Thorne & John Archibald Wheeler $\S\S$ 8.4 Tensor Algebra in Curved Spacetime, Box 8.4 Tensor algebra at a fixed event in an arbitrary basis.

See also the lecture notes Vectors and Dual Vectors PDF

---

Edit to add graphics.

The first image depicts a vector (blue) resolved onto a covariant basis (red and green), and onto a contravariant basis (cyan and magenta). The basis 1-forms dual to the covariant basis are likewise depicted in cyan and magenta. They are "surfaces" of constant coordinate value. So, if the red line is tangent to the coordinate inducing the red basis vector, the cyan lines are tangent to the subsequent coordinate curves "parallel" to the red line, etc. Notice that the dual (contravariant) basis vectors are orthogonal to their corresponding covariant basis vectors. Also observe that the contravariant basis vectors are orthogonal to their corresponding 1-form surfaces. The same geometric object was used to draw both the 1-forms and the contravariant basis vectors. They were just passed to different functions.

The second image depicts a vector "resolved" onto the covariant basis in terms of both covariant and contravariant components. This requires some scaling which is described in Theoretical Physics, By: Georg Joos, Ira M. Freeman

---

Edit to add: The following image shows equivalent forms of a the component matrix associated with a change of coordinate induced bases. It is by no means exhaustive. It would be too much effort to translate it from Mathematica to LaTeX where I produced it. Of course, one needs context in order to expand the single row and single column forms to show their equivalence with the other forms.