1

I am usually skeptical of riddles online that have to do with Physics but this one struck me as they had an oddly specific answer to it. So my question is for the following picture:

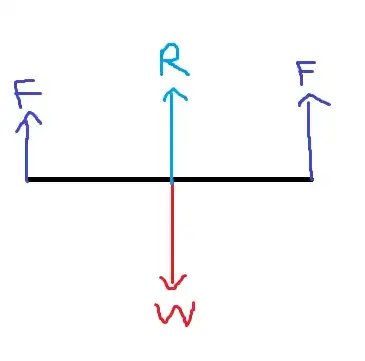
enter image description here

I simplify a bit with placing the two men at the very ends and the middle man at the exact center of the log in line with its center of mass(considering log to have weight $W$). I know I have to find the normal reaction force on the middle man, suppose it to be $R$ and I know by solving moments that the normal reaction for two men on the sides are equal, both equal to suppose $F$. Now even if I solve using both resolving vertically and using moments I end with the same result of : $$2F+R=W$$ Even if I consider the two men at the ends to be not exactly at the ends but at a length $l$ from either side, we get using moments $2Fl+Rl=Wl$ which again ends up as $2F+R=W$.

So my question is, how did they get the result of the middle man having 25% more normal reaction force and if I'm missing any results here. Also, is it really possible to compare the normal reaction forces between the three men?

Tausif Hossain
  • 2,958

3 Answers3

4

This is a problem of Mechanics of solids. You are right in using the concept of moment equilibrium to get the equation 2F+R=W. But the thing is that this is a statically indeterminate problem. I'll tell you why, in the above equation you have two unknowns F&R. So for two unknowns you need two distinct equations, but here if you apply the other static equation of equilibrium (sum of all downward forces = sum of all upward forces) , you get the same equation W =2F + R. Statically indeterminate problems are solved by basically two methods: force method and displacement method. I have a similar problem in my book solved by Castigliano's theorem. I will present the solution briefly. Let the length of wooden log be 2a. We can consider the situation in riddle as a beam of negligible self weight, under the action of the same weight W but with it being uniformly distributed over length 2a, having load intensity w, such that w*2a = W. Also the three men are replaced in beam analogy by three rigid(non-deformable) supports.

Now, under the condition that the two men on the ends are both totally extreme i.e 'a' distance away from the middle man and that they both exert equal force F on the log, then the man in the middle will have to exert a force R= 5/4 wa = 5/8 W; since w*2a =W.

F will be equal to 3/8 wa = 3/16 W. Now, 2F=3/8 W & R-2F = 2/8 W= 0.25 W. Thus, the force applied by middle man exceeds the combined effort of the other two men by 0.25W or in other words the effort applied by middle man in lifting load W is 25% more than the effort of other two combined.

Mohammad Nayef
  • 309
1

Unless there is more to the puzzle than the image suggests, it seems to me fairly straightforward to show that the two outside men carry an equal amount of weight and the inside man carries any weight not carried by the outside men. If either outside man carries more weight than the other, the log tips over. The middle man can carry any amount of weight (he could even not be there).

Physical Mathematics
  • 1,046
  • 8
  • 15
1

This riddle is wrong because a log is far stiffer than a person, so the appropriate assumption is that the log does not bend, but people are squished down by an amount proportional to the weight they carry (replace people with springs).

If the log remains horizontal and does not deflect, then each person is squished by the same amount, and thus each carries $1/3$ of the total weight.

John Alexiou
  • 40,139