3

I understand that before sunrise, twilight shows several colors, so I'm looking for the average color (wavelength) and brightness (lux) of light that is being projected from the sky before the sun visibly rises.

enter image description here

I've seen a similar question here, but the resulting formula is a) apologies, way over my head (I'm a physics fan but not a physicist) and b) doesn't appear to take into account the Rayleigh scattering of sunlight seen before sunrise or atmospheric refraction and how we see the sun before it's above the horizon line.

I've come to learn that there are a lot of variables that can affect this color/brightness including latitude, elevation (longitude), time of year, weather conditions, pollution, particles in suspension, etc. -- So for simplicity's sake, the viewer would be at sea level on the equator on the morning of the Summer Solstice, and the sky would be clear across the earth. (If I'm missing another key variable, please let me know)

Twilight spans over time in three light phases that are all measured by the degree of the sun below the horizon:

  • Astronomical Twilight (from -18° to -12°)
  • Nautical Twilight (from -12° to -6°)
  • Civil Twilight (from -6° to 0/-0.59°) (which contains Blue Hour)

It ends when Sunrise begins (which contains Golden Hour). Because of atmospheric refraction sunlight bends around the earth, so technically the sun is visible before it gets to 0° to the horizon (roughly 35.4 arcminutes higher = 0.59 degrees).

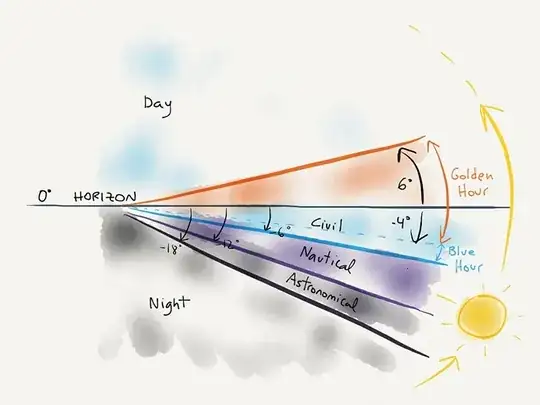
A representation of morning twilights, golden hour and blue hour.

My question: What is the average color (wavelength) and brightness (lux) of light for each degree of the sun below the horizon starting at Astronomical Twilight (-18°) and ending just before the moment of sunrise (~0.59°)?

This will allow me to create a proper gradient that will show this light change over time. In short, I'd like to fill out this table:

enter image description here https://codepen.io/Rogue75/pen/OERKop

Davbog
  • 137

1 Answers1

2

There are illuminance data per half-degree of solar elevation at twilight available on Paul Schlyter's page, but nothing on colour spectrum. Computer graphics researchers (Bruneton & Neyret) have published code to calculate atmospheric scattering, but not so far as I know tested against detailed reality.

There are comprehensive per-minute nanometre experimental spectra available in the supplementary material of a paper by University of Pennsylvania researchers Spitschan et al. (2016).

"Average" wavelength seems to be a less common quantity of illumination than correlated colour temperature or CIE colour co-ordinates. I've made an attempt to compute wavelength from the Pennsylvania summer data, selecting two rural moonless mornings out of the several days monitored. Not that the moon makes much difference, but you can see the effect of daytime cloudiness. The spectra also suggest the ozone Chappuis band eliminates about half of orange light during the 'blue hour'; it also looks like double Rayleigh scattering produces a general bias to blue.

The change in sky colour shows up less in photopic (cone sensitivity) 'mean' wavelength, since that's concentrated around green, than it does in physical irradiance, so I'm including both, together with scotopic (rod sensitivity) illuminance. The irradiance data is for between 380 and 780 nm, and therefore includes some near infra-red. Although there's a spectral peak below 500 nm (ie in the blue), the 'average' never reaches that because of a long red tail. The redness during night is presumably airglow.

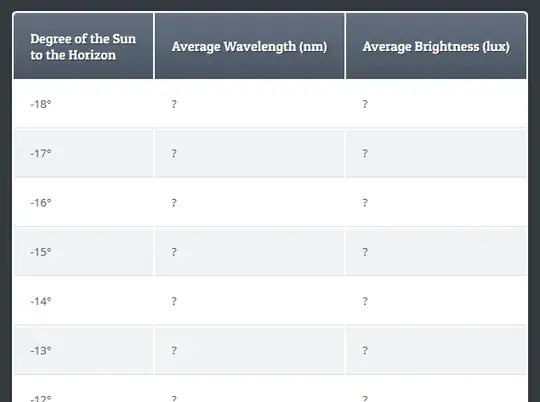
Sun °,irradiance,   scot lx,   phot lx,photopic nm,irr nm
 -20,  0.000004,    0.0014,    0.0008, 564.3, 601.7
 -19,  0.000005,    0.0017,    0.0009, 563.8, 605.7
 -18,  0.000005,    0.0016,    0.0009, 563.5, 604.0
 -17,  0.000005,    0.0016,    0.0008, 563.3, 603.0
 -16,  0.000003,    0.0010,    0.0005, 563.0, 593.0
 -15,  0.000004,    0.0017,    0.0008, 559.0, 570.7
 -14,  0.000006,    0.0031,    0.0011, 552.8, 553.9
 -13,  0.000011,    0.0058,    0.0016, 546.8, 541.0
 -12,  0.000020,    0.0106,    0.0026, 542.2, 535.9
 -11,  0.000047,    0.0247,    0.0060, 540.7, 540.4
 -10,  0.000117,    0.0650,    0.0147, 537.6, 531.6
  -9,  0.000273,    0.1564,    0.0347, 536.7, 526.0
  -8,  0.000761,    0.4549,    0.1016, 536.6, 520.4
  -7,  0.002138,    1.3136,    0.2970, 536.8, 517.2
  -6,  0.006553,    4.0423,    0.9328, 537.5, 518.1
  -5,  0.018006,   11.1915,    2.6195, 537.9, 518.0
  -4,  0.052251,   32.5612,    7.7281, 538.4, 519.1
  -3,  0.146334,   90.3824,   22.2753, 539.8, 525.1
  -2,  0.352731,  218.6244,   55.4249, 540.7, 526.1
  -1,  0.763037,  474.1386,  125.0604, 542.1, 526.6
   0,  1.580555,  962.4795,  272.0179, 544.5, 532.2
   1,  2.772255, 1666.0518,  500.7170, 546.5, 537.4
   2,  4.411440, 2523.4746,  815.0906, 549.0, 548.1
   3,  6.702043, 3671.5632, 1254.1349, 551.0, 555.6
   4,  9.416510, 5084.9744, 1773.6052, 551.7, 557.2
   5, 12.865984, 7436.9430, 2507.0312, 550.2, 545.2
   6, 17.437111, 9649.4890, 3420.7512, 551.9, 553.3
   7, 20.121992,11071.6979, 3965.8271, 552.3, 553.7
   8, 26.330863,13829.1131, 5235.3776, 554.1, 562.6
   9, 45.112879,21760.3774, 9179.4651, 557.6, 576.3
  10, 36.358187,18189.3212, 7454.5144, 556.3, 572.2
  11, 39.137271,20176.6702, 8084.3033, 555.5, 567.0
  12, 61.641958,30708.4968,12903.1196, 557.0, 573.3
  13, 77.212419,37803.7065,16239.1084, 557.7, 576.0
  14, 90.655367,43652.7913,18982.5532, 558.3, 577.2
  15, 93.396421,45058.8386,19410.2871, 558.3, 575.2
  16,112.860479,53569.4518,23508.1913, 558.8, 578.0
  17,121.886868,60050.7316,26070.7039, 557.8, 575.6
  18,132.862405,65464.2749,28434.6294, 557.9, 575.4
  19,120.301796,59054.1295,25659.3754, 557.8, 576.5

Converting to RGB

Mean wavelength is only one dimension, whereas you generally need two (besides luminosity) to capture colour, such as Lab*, Luv, LCh. (Nevertheless, sky colour can be summarised from a correlated colour temperature.) To approximate RGB colour dependence on solar elevation, I'd combine the Pennsylvania rural spectra with cone sensitivities from here, probably the 10° versions since we're dealing with wide-angle low-light conditions. (I can add that table here later, as am doing it for an art project anyway.) Fig 4 of the Pennsylvania paper already renders a clear shift from white daylight to blue twilight, using a more complex transformation.

Both the Pennsylvania and Granada research decompose spectra into six dimensions, each of which could also be converted to a RGB value, and an elevation-dependent curve fitted to their relative weights. The Granada data has the advantage of being specifically sky-light rather than total daylight on a horizontal sheet, but I'm not sure it's available for a range of solar elevations or zenith angles, particularly those in twilight. Diakite-Kortlever et al (2023) summarises more recent developments.

Cedric Knight
  • 136