Can dimensional regularization be viewed as a soft version of a Wilsonian cutoff?

Question

In the Wilsonian picture of renormalization, a quantum field theory is defined to have degrees of freedom only up to an energy scale $\Lambda$. The results of low-energy experiments shouldn't change as we lower $\Lambda$, as long as we change the parameters in the action to compensate for the loss of the high-energy modes. Quantitatively, we have $$S_{\Lambda'}[\phi] = S_{\Lambda}[\phi] + \log \int_{\tilde{\phi} \in (\Lambda', \Lambda)} \mathcal{D} \phi \, e^{iS_{\Lambda}[\phi]}$$ which expresses the fact that the partition function is invariant, $$\int_{\tilde{\phi} \in (0, \Lambda')} \mathcal{D}\phi\, e^{i S_{\Lambda'}[\phi]} = \int_{\tilde{\phi} \in (0, \Lambda)} \mathcal{D}\phi\, e^{i S_{\Lambda}[\phi]}.$$ Then we have scale-dependent couplings $g(\Lambda)$.

On the other hand, in 'continuum RG' techniques such as dimensional regularization, there is no high-energy cutoff. Instead, we perform some mathematical trick to assign finite values to the unbounded integrals. Sometimes, but not all of the time, the trick we use will introduce an arbitrary mass scale $\mu$, yielding scale-dependent couplings $g(\mu)$.

There are lots of questions on this site about how these two approaches are related, with the usual answer being that there's no relation whatsoever. But I suspect the two views are really the same!

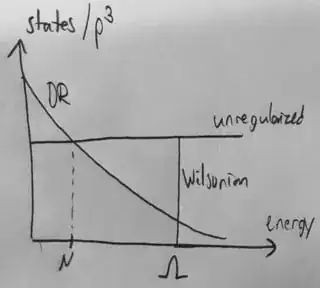
Consider some loop integral in an unregularized theory, $$I = \int d^4 p\, (\text{stuff}) \sim \int_0^\infty p^3\, dp \, (\text{stuff)}.$$ In the Wilsonian picture, the integral would be finite by a hard cutoff, $$I \sim \int_0^\Lambda p^3\, dp \, (\text{stuff)}.$$ In dimensional regularization, we instead work in arbitrary dimension, giving $$I \sim \int_0^\infty p^{d-1} dp \,(\text{stuff}).$$ Then if we take $d < 4$, there are more degrees of freedom with lower energies, and less degrees of freedom with higher energies. If we say we have equality at energy $\mu$ (and this must be true, by dimensional analysis), then dimensional regularization is just doing a smoother version of the hard Wilsonian cutoff, with $\mu \sim \Lambda$!

To clarify, here's a sketch of how the number of degree of freedom at some energy changes in each of these schemes.

Is this picture valid? Are all continuum RG methods secretly Wilsonian? Are there any references where people discuss these ideas?

Answer 1

To address your broader question, let me point out that it's not necessary to think that in Wilson QFT "a quantum field theory is defined to have degrees of freedom only up to an energy scale $\Lambda$". You can imagine that the degrees of freedom exist on all scales, and it won't matter, as long as the energy/action functional only depends on the long distance scales.

THE REST OF THIS ANSWER IS MISLEADING. See Does the angular measure matter in dimensional regularization?

To your narrower question: Yes, you can think of dimensional regularization as a softer version of a momentum cutoff. (I like this perspective because it's not necessary to think of dimensional regularization as actually interpolating between spaces of different dimensions. You can get away with this in limited circumstances, but in general, it's just confusing. Spinor representations, for example, don't really adapt well to fractional dimensions.)

The main point of dimensional regularization is that you can examine the singularities of momentum integrals by replacing the usual momentum measure $d^np$ with $\big(\frac{\mu}{|p|}\big)^{\epsilon} d^np$. This is still a measure on the functions on $\mathbb{R}^n$, but the extra powers of $|p|$ in the denominator suppress the high momentum modes in comparison with the low momentum modes. Then you impose renormalization conditions, and remove the cutoff by sending $\epsilon \to 0$.

Note: This isn't quite the textbook definition of dimensional regularization because I haven't bothered to analytically continue the angular measure. For example, in the 'textbook' dimensional regularization, one finds $$\int \frac{d^{4-\epsilon}k}{(2\pi)^4} \frac{1}{(k^2 + \Delta)^2} = \frac{1}{(4\pi)^2} \big(\frac{2}{\epsilon} - \log(\Delta) + \gamma + \log(4\pi) + O(\epsilon)\big).$$ In the variant I'm using here, $$\int \frac{d^4k}{(2\pi)^4} \frac{(\mu/|k|)^{\epsilon}}{(k^2 + \Delta)^2} = \frac{1}{(4\pi)^2} \big(\frac{2}{\epsilon} + \log(\frac{\mu^2}{\Delta}) + O(\epsilon)\big).$$

I don't think this makes any meaningful difference. The angular measure's $\epsilon$-dependence creates some terms constant in $\epsilon$, but it doesn't change the dependence of the integral on external momenta. But as you can see, it does change the expressions that appear at intermediate stages, before you impose renormalization conditions.

Answer 2

I don't have a precise answer, but I think that the way people think about the relation has changed over time and between subfields. In condensed-matter physics, everyone was always aware that the field-theory picture breaks down at the atomic scale, so its predictions become useless at sufficiently high energies (which are actually experimentally accessible). So CM people have always thought about RG in the Wilsonian cutoff sense (even before Wilson himself actually formalized the concept) as what's really going on "behind the scenes", even when they use dim reg as a practical calculational shortcut.

On the other hand, decades ago, before anyone really worried about quantum gravity, it was believed that high-energy QFTs could in principle give an exact description of physics at all energy scales, so high-energy physicists didn't really like using the cutoff conceptualization for "fundamental" theories like the SM - it seemed contrived and artificial, as there's no known natural value for the cutoff. (I guess they were more okay with it in explicit effective field theories like the Fermi beta-decay theory, where there is a natural cutuff.) So they preferred the dim reg approach, as it's mathematically shady and physically mysterious, but at least it doesn't invoke an explicit cutoff.

I think the two schools of thought have greatly converged in recent decades, because (a) Wilson made great progress in making the previously-hazy notion of an energy cutoff much more precise and rigorous, and (b) people starting taking quantum gravity seriously, and accepting that the SM will certainly break down at the Planck scale (if not long before). So now people in both camps tend to think of QFTs as being long-wavelength effective theories with unknown "microscopics", and that the two regularization formalisms are probably completely equivalent (although I don't think anyone's proven that rigorously). But as a historical holdover from before this "synthesis", high-energy physicists tend to present the two formalisms separately and not focus on their conceptual connections - because that's how they learned it themselves.

Anyway, sorry to not really answer your real question.

Answer 3

Even high-energy physicists are interested in effective ("Wilsonian") low energy theories, as some calculations (eg bound states) are much easier in effective theories.

But they prefer dimensional regularisation as it is the easiest scheme that preserves Lorentz and gauge symmetries without which one is easily led astray in the conclusions.

Take a look eg at this review by Georgi