3

A few months ago I was discussing the spaghettification phenomenon with my wife, just for the fun of it. This was when the mass of the supermassive black hole from M87 hit the news. The black hole was meant to have $6.7\times 10^9$ solar masses, so I thought it would be fun to figure out at which distance the tidal forces become so great, that the forces between your head and feet start getting... uncomfortable.

I defined the distance from feet to head to be 2 m, the head having a mass of 10 kg and one foot having a mass of 2.5 kg (I didn't research the numbers, I just did some wild guesses).

So, the force between head and foot should be:

$$G*m_B*m_H \over (d+2)^2$$ $$-$$ $$G*m_B*2*m_F \over d^2 $$ where $d$ is the distance from foot to the black hole, $m_B$ is the mass of the black hole, $m_H$ the mass of the head and $2*m_F$ the mass of the feet. Assuming you fall with the feet first.

This is one of the plots I made: 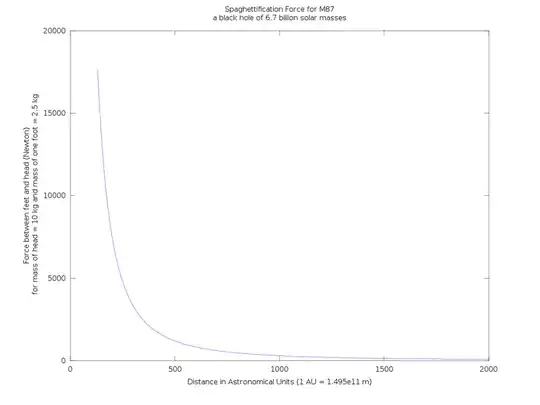Spaghettification: Human vs. M87 (note: the plot only takes the mass of one foot into account.)

I made up this short octave script to plot the forces on this values with the distance in AU as the free variable and thought "ouch, that's gonna hurt pretty soon". I haven't checked which part of the body will rip off first at what forces though...

Anyway, what I wanted to know is: Do my calculations make sense? Is my math correct?

ProfRob
  • 141,325
Alexander Janssen
  • 131

3 Answers3

2

It's actually well-known that it's the exact opposite: if you want to make spaghetti big black holes are not interesting, small black holes are. Let's go through why.

So what you've got is a Newtonian expression for something that we do slightly more easily with calculus, $$\Delta a = \Delta\left(-\frac{GM}{r^2}\right) = \frac{2GM}{r^3} \Delta r.$$

As another comment noted, $r$ here needs to be taken to be about 130 AU and thus this is a very very large denominator, while the $\Delta r$ we can take as being about one meter. The acceleration at such distance $r$ can then be calculated as $10^{-10} \text{m}/\text{s}^2$ or so, or one hundred-billionth of the acceleration of gravity on Earth, which can be used to stretch you for example if you hang from monkey-bars. You wouldn't notice this acceleration at all at the event horizon. (Once you have entered it of course you might well be spaghettified as well, but once you have entered an event horizon you have much bigger problems to worry about.)

This form also allows us to see that since the Schwarzschild radius scales linearly with mass, the spaghettification force $\Delta a \propto 1/M^2.$ So if you consider just a 1-solar-mass black hole the Schwarzschild radius is about 3km large which sounds small, but it allows you to get much closer: the tidal forces there are something like $10^{10} \text m/\text s^2,$ or a billion times stronger than the acceleration of gravity on Earth. So far before you actually get into the event horizon you will be pulled apart in that scenario.

CR Drost
  • 39,588
2

Two factoids to add to Chris Drost's answer.

Firstly, although small black holes exert stronger tidal forces before you get to the horizon, that is of little concern since the time between when the forces become uncomfortable and when you get splattered on the singularity is (a) independent of the black hole mass and (b) too short for you to even perceive it happening.

So let us start from Chris's formula $$\Delta a = \Delta\left(-\frac{GM}{r^2}\right) = \frac{2GM}{r^3} \Delta r.$$ and assume this gets uncomfortable when $\Delta a = 50$ m s$^{-2}$. Further, assuming that $\Delta r \sim 1$ m (for a human), then the "discomfort radius" $r_d$ is $$ r_d \sim \left(\frac{GM}{25}\right)^{1/3}\ {\rm metres}$$

The relationship between the proper time to fall to the singularity from radial coordinate $r$ (for falling into a black hole from a long way out) is $$ \tau = \frac{2r^{3/2}}{3r_s^{1/2} c}\, ,$$ where $r_s = 2GM/c^2$.

If we thus let $r= r_d$, then the time you are in discomfort for is $$\tau_d \sim \frac{2}{3c} \left[ \frac{(GM/25)^{1/2}}{(2GM/c^2)^{1/2}}\right] = \frac{\sqrt{2}}{15}\ {\rm seconds}\, .$$

The nerve impulses wouldn't have time to travel to your brain.

Secondly, it's called spaghettification because there are two tidal forces at work. The second is due to the component of the radial gravitational pull that is resolved tangential to the radial vector. i.e. Gravity acts towards the centre of the black hole, but that direction varies across the "width" of the falling body.

That compression force is given (approximately, again assuming Newtonian physics) by $$F_{\rm compress} \sim 2 \frac{GMm}{r^2} \sin \theta\, ,$$ where $\theta \sim \Delta r / r $ and this time, $\Delta r$ is the half-width of the falling body.

Thus there is a compressive force in the tangential direction that is roughly equivalent to the stretching force in the radial direction. Hence spaghetti.

ProfRob
  • 141,325
1

I have two feet, therefore I think the force will be double what is calculated.

However, I don't have a head weighing 10kg, therefore I think the force will be half what is calculated. (see http://hypertextbook.com/facts/2006/DmitriyGekhman.shtml and others)

Therefore I think I agree with the conclusion, but for slightly different reasons.

Antony
  • 11