Twin's clock slowing down

Question

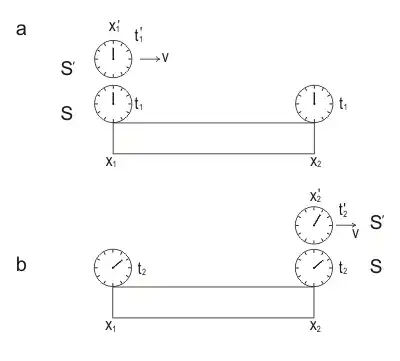
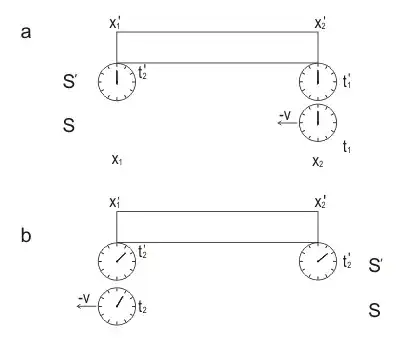
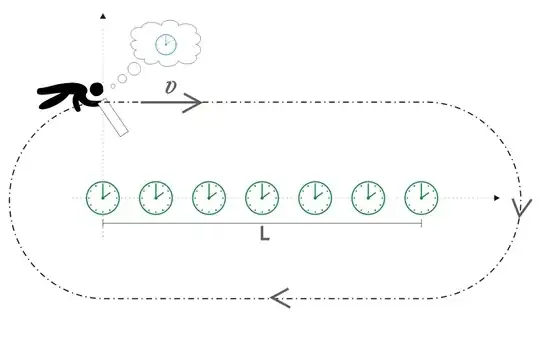
This question is not same as explaining Twin paradox. This question does expect that the travelling twin will age less. The question in here is what causes the travelling clock to slow down, which is verified at the end of the journey. If the cause is acceleration, then why the consecutive accelerations in opposite directions have opposite effects on clock speed.

I am looking for conceptual description, not a lot of mathematics.

Again, this is long question, please be patient.

Down voters, please share your thoughts as well.

Start -

Two twins are on earth with their clocks synchronized.

One stays on earth, the other makes a fast and long, quick round trip journey and then they compare the clocks.

Q1 - Is it expected that the trip making clock will be far behind the one that was left on earth? Obviously if it is true, then the difference will depend upon how fast and how long the trip was.

If the answer to above is true, then we know that the clock of the travelling twin did really slow down.

Doesn't this tell us that the ticking of clock was actually slowed down due to initial acceleration, then continued to run at slower rate (as compared to the one on earth), then sped up again during retardation at far end.

Suppose the travelling twin remained at 0 relative speed wrt earth for a day or so. During this day or so, both twins can verify that the clock of travelling twin is now behind, but tick rate is same during that day. Meaning the travelling clock was really ticking at slower rate.

Then the travelling twin started accelerating back toward earth. The clock of this twin would slow down again.

The retardation just before far end and the acceleration in start of return journey, are actually acceleration in same direction.

But the first part of this acceleration (retardation) sped up the clock, and second part slowed it down.

When the travelling twin reduces speed again before reaching earth. This reduction in speed again speeds up his/her clock so that the tick rate is same for both twins now. But the difference in clock times would be double of what it was noted at the far end. Consider all accelerations same rate.

Q2 - Do we really understand how the "same direction" acceleration sometimes slows down the speed and sometimes speeds them up.

But if answer to Q1 is yes, then this slow down and speeding up of clocks always seems to be equal and opposite if you consider any two consecutive changes in speed that pass through the 0 relative speed point.

Or, there is no real change in tick rate, and the slowdown is just relative and perception? And when the travelling twin comes back to earth, its clock will show same time as that of the other twin?

Answer 1

@kpv, from the comments I'd say don't worry, there are plenty of smart people around here who can't make heads nor tails of what those who claim to understand relativity are saying. The admonition to go away and read is not sufficient if one desires dialog about what has already been read and how it should be interpreted, particularly if multiple sources contradict or struggle to be clear (as they do).

The explanation for the asymmetry of time dilation in SR is that the Earth (or the solar system or fixed stars, in the appropriate cases) is being employed as a "preferred frame", which happens always to have the (relatively) faster rate of time than the moving object under consideration.

This preferred frame has the character of treating a sufficiently large amount of the massive environment as static.

The scale of environment that has to be taken into account depends on the scale of the times and distances involved and the necessary level of precision, so as to correct if necessary for effects of things that are moving within the frame, such as the movement and rotation of planets or solar systems.

And a close analysis shows that all practical applications of relativity fall back on a preferred frame of using a larger and larger environmental scope. In other words, it does not treat two interacting objects (like twins) as isolated in a vacuum, moving only relative to one-another (which is when the twin paradox arises).

It recognises that one twin stays anchored on Earth (moving at most at a modest speed relative to anything else nearby), and one goes into space at near-light speed, where it can be said decisively which one is moving at the higher speed relative to the wider environment, and therefore it can be said decisively which one should be treated as suffering the slowing of its clocks.

The Hafele-Keating experiment, for example, had to correct for the rotation of the Earth in order to account for time discrepancies which differed according to which way around the Earth you travelled. A rotation of the Earth which can only be said to be present if you use the solar system or fixed stars as a reference point for the rotation. I assume if planes were flown in different directions around the Sun, the Sun would similarly have to become a rotating body inside and relative to a much wider galactic reference frame.

Note that this is not the same as an "absolute frame", since we are still measuring time and motion relatively, and there is no support for the notion that an absolute frame or an independent aether exists by which motion can be judged relative only to space (and not to other things in it). Nor does it contradict the notion that local laws are invariant under motion, as the local laws remain in the same relation under movement (but clocks will be affected depending on how that movement relates to the environment).

Note also that (and in my experience this is bound to raise hackles amongst some) my take on time dilation is that it is equivalent to (and indistinguishable from) the slowing down in the rate of fundamental physical processes.

It is often counter-alleged in very woolen terms that it is "not clocks that have slowed down" but "time itself", but in my view this simply moves the argument away from talking about something that is real, experimentally testable (and indeed already tested), and familiar to us all, into a discussion about what "time itself" is (and how this view differs in its implications from talking about the rate of physical processes, and clock machines that are based on them).

I struggle to give an account of what 'time itself' is in the abstract, and the proponents of that view often do no better other than to assert it's truth axiomatically without being capable of further explanation or differentiation, so if there is an underlying difference it is seemingly not one that anyone can articulate.

Answer 2

Indeed, if we assume, that clock dilated due to absolute motion, the quirky “paradox” turns into very simple effect.

At least – let’s try not to change frame. The paradox disappears, as soon as one of the twins admits, that he was in motion in the frame of the other. In his case this observer will conduct measurements in another way and would see, that the clock “at rest” is running not slower, but $\gamma$ times faster than his own.

The problem with the paradox in the framework of the SR is that any observer never admits, that he moves. An observer tends to ascribe himself state of “proper rest” and to look at the problem from his “rest frame”. That means, the both twins think about themselves as if they are at rest, even though if they move relatively to each other. That leads to many confusions and quirky resolutions.

Please note, that in special relativity, the observer "at rest" measures events against an infinite latticework of synchronized clocks, or his "rest frame".

We can demonstrate time dilation of the SR in the following experiment below. Moving with velocity $v$ clock $C’$ of reference frame $S’$ measures time $t'$. The clock passes past point $x_{1}$ at moment of time $t_{1}$ and passing past point $x_{2}$ at moment of time $t_{2}$.

At these moments, the positions of the hands of the moving clock and the corresponding fixed clock of reference frame $S$ next to it are compared.

Let the arrows of moving clock measure the time interval $\tau _ {0}$ during the movement from the point $x_ {1}$ to the point $x_ {2}$ and the hands of clocks 1 and 2, previously synchronized (Einstein synchrony convention) in the fixed or “rest” frame $S$, will measure the time interval $\tau$. This way,

$$\tau '=\tau _{0} =t'_{2} -t'_{1},$$

$$\tau =t_{2} -t_{1} \quad (1)$$

But according to the inverse Lorentz transformations we have

$$t_{2} -t_{1} ={(t'_{2} -t'_{1} )+{v\over c^{2} } (x'_{2} -x'_{1} )\over \sqrt{1-v^{2} /c^{2} } } \quad (2)$$

Substituting (1) into (2) and noting that the moving clock is always at the same point in the moving reference frame $S'$, that is,

$$x'_{1} =x'_{2} \quad (3)$$

We obtain

$$\tau ={\tau _{0} \over \sqrt{1-v^{2} /c^{2} } } ,\qquad (t_{0} =\tau ') \quad (4) $$

This formula means that the time interval measured by the fixed clocks is greater than the time interval measured by the single moving clock. This means that the moving clock lags behind the fixed ones, that is, it slows down.

However, time in reference frame from the “point of view of the single clock” is running $\gamma$ times faster instead. If moving observer compares his clock readings successively with synchronized clocks of reference frame $S$ he moves in, he will see, that these clocks change readings $\gamma$ times faster. But, if the observer changes frame and places two spatially separated clocks of his frame $S'$ at points $x'_{1}$ and $x'_{2}$ then every single clock of reference frame $S$ that moves from $x'_{1}$ to $x'_{2}$ will flash $\gamma$ times slower.

The animation below vividly demonstrates that:

We can also look at the problem through the prism of the Transverse Doppler effect (diagram is below).

An observer can measure Transverse Doppler effect of source of radiation. The Transverse Doppler effect reflects rate of relatively moving clock. We can imagine, that observer moves along the row of synchronized clocks of reference frame $S$ and looks at these clocks through a telescope. Let all clockfaces of these clocks are highlighted in green monochromatic light.

What color of the clocks the observer will see? If he thinks, that he is at rest, he will direct his tube at right angle to the line that connects clocks. Then he will see, that clock rate of every single clock is $\gamma$ times slower. Color of each clockface will be red, or $\gamma$ times redshifted. However, during reversal, when he moves at half – circle around the last clock, he will not see any light, because he cannot ascribe himself state of rest then. Due to aberration, he must always keep his telescope at angle $\sin \alpha = v/c$

He must remember, that he himself moves in the reference frame $S$. He must take aberration into account and turn his telescope forward at relativistic aberration angle $\sin \alpha = v/c$. He will always, all the time will see that the clocks of reference frame $S$ will be of blue color, or $\gamma$ times blueshifted due to Transverse Doppler effect.

$$f_0= \frac {(1+\cos\theta_s\cdot v/c)}{\sqrt {1-v^2/c^2}}f_s$$

We see, that if the source emits at right angle in its frame ($\cos\theta_s = 0$) frequency will be $\gamma$ times blueshifted.

The observer who makes U - turn around the source (or rotates around the source) will always see blueshift of frequency, i.e. that source's clock is running faster. Source always emits at right angle. He cannot see any other frequency shift, only blue one.

This way moving observer will see, that each individual clock of reference frame $S$ is ticking $\gamma$ times faster, since his own clock dilates, and the set of clocks, if he looks at them successively, runs faster. He can explain that by dilation of his own clock, since he moves himself in the reference frame $S$.

See Transverse Doppler Effect in Wikipedia. https://en.wikipedia.org/wiki/Relativistic_Doppler_effect

or Mathpages http://www.mathpages.com/home/kmath587/kmath587.htm