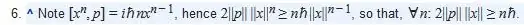Stone-von Neumann theorem

Question

According to Stone-von Neumann theorem, any two canonically conjugate self adjoint operators following the relation: $$[\hat{q},\hat{p}]=i\hbar$$ cannot be both bounded. I am confused about how we prove this part and what does it mean physically? Can anyone explain?

Answer 1

I commented that the Stone-von Neumann theorem is not a proof for the statement in the beginning of the question. The original proofs of the Wielandt-Wintner theorem (incidentally proved only in 1947-1948, while the Stone-von Neumann theorem had a satisfying proof by von Neumann already by 1931) are found in:

Wintner, A. - The Unboundness of Quantum-Mechanical Matrices (1947, The Physical Review, Vol. 71, p. 738-739)

Wielandt, H. - Über die Unbeschränktheit der Operatoren der Quantenmechanik (1948, Mathematische Annalen, p. 21).

The essence of Wielandt's proof is note 6 of the quoted Wiki page:

The significance of having unbounded operators of coordinate and momentum on the real axis (1D) is that the particle's "quantum motion" is unrestrained, in the sense that either the coordinate or the momentum can be measured to an arbitrary high value (infinite in the limit), i.e. mathematically, unbounded operators do not have a bounded spectrum.

Answer 2

Theorem: If two (not necessarily self-adjoint) bounded operators $\hat{q}$ and $\hat{p}$ on a Hilbert space satisfy the CCR $$[\hat{q},\hat{p}]~=~i\hbar~{\bf 1}, \qquad i\hbar~\in~\mathbb{C},\tag{1}$$ then $i\hbar=0$.

Indirect proof: (This is essentially the proof of Ref. 1.) Assume $$i\hbar~\neq~ 0.\tag{2}$$ Since $\hat{p}$ is bounded, we may shift $$\hat{p}^{\prime}~:=~\hat{p}+ b{\bf 1}\tag{3}$$ by a finite positive amount $b>0$, so that $\hat{p}^{\prime}$ is an invertible operator, and so that $\hat{p}^{\prime}$ and $\hat{p}^{\prime -1}$ are both bounded operators. Note that the primed operator $\hat{p}^{\prime}$ also satisfies the CCR (1). Let us drop the prime notation from now on. The spectra $$\sigma(\hat{q}\hat{p})~=~\sigma(\hat{p}\hat{q}\hat{p}\hat{p}^{-1})~=~\sigma(\hat{p}\hat{q})\tag{4} $$ of the bounded operators $\hat{q}\hat{p}$ and $\hat{p}\hat{q}$ must be equal bounded sets. On the other hand, the CCR (1) shows that the spectra are shifted $$\sigma(\hat{q}\hat{p})~\stackrel{(1)}{=}~\sigma(\hat{p}\hat{q}) +i\hbar\tag{5}$$ The only way that the eqs. (2), (4) & (5) could be not mutually contradictory is if the spectra are the empty sets. However, this contradicts the general fact (mentioned on e.g. Wikipedia and MO.SE) that

Fact: Every bounded operator has a non-empty spectrum.

$\Box$

Remark: If we additionally assume that $\hat{q}$ and $\hat{p}$ are self-adjoint, we do not need to use the above fact. Then the commutator (1) is anti-selfadjoint, so that $\hbar\in\mathbb{R}$ must be real. Moreover the bounded operator $$ \hat{s}~:=~\hat{q}\hat{p}-\frac{i\hbar}{2}~\stackrel{(1)}{=}~\hat{p}\hat{q} +\frac{i\hbar}{2}~=~\hat{s}^{\dagger}, \tag{6}$$ is selfadjoint, and hence (from the spectral theorem) has a non-empty real spectrum $$ \emptyset~\neq~\sigma(\hat{s})~\stackrel{(6)}{=}~\sigma(\hat{q}\hat{p})-\frac{i\hbar}{2}~\stackrel{(1)}{=}~\sigma(\hat{p}\hat{q}) +\frac{i\hbar}{2}, \tag{7}$$ which is eq. (5) without the loophole of empty sets. $\Box$

References:

1. A. Wintner, Phys. Rev. 71 (1947) 738.

Answer 3

Conjugate variables/operators are related by Fourier transform, that is, the (quantum) states of one observable are the Fourier transform of the other's and as such, only one of them can have a compact support (unless it's a zero function). This is known as the Uncertainty relation in Fourier transforms. Intuitively, it means the spread of a variable and its Fourier dual are inversely proportional, which physically translates into e.g. the position being localized (concentrated) and the momentum delocalized (spread out). For a proof approach see Qmechanic's answer.

Physically, all such types of variables/observables are incompatible (non-commuting $XP - PX \neq 0$, where $P \propto F^{-1} X F$ with $F: L^2(\mathbb{R}) \to L^2(\mathbb{R})$ ), as in they cannot be measured simultaneously to arbitrary precision. In other words, the uncertainties in the two variables are always bounded by the average of their commutator (even if you made the measurements separately on an ensemble of infinitely many identically prepared quantum systems). These uncertainties are an intrinsic property of any quantum state.