Electric field of uniformly moving charge ; misprint in Feynman textbook? (28.3)

Question

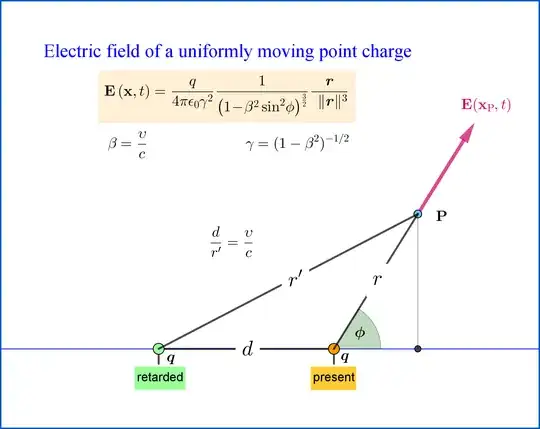
I doubt about formula (28.3) from this Feynman's lecture.

$$\textbf{E} = - \frac{q}{4 \pi \epsilon_0 } \Big{[} \ \frac{e_{r'}}{r'^2}+ \frac{r'}{c} \frac{d}{dt} \Big( \frac{e_{r'}}{r'^2} \Big) + \frac{1}{c^2} \frac{d^2}{dt^2} e_{r'} \ \Big{]}.\tag{28.3} $$

Consider a charge moving along axis $OX$ with constant speed $v$. Let us consider field at a point on the $OX$. Then formula simplified as follows

$$\textbf{E} = - \frac{q}{4 \pi \epsilon_0 } \Big{[} \ \frac{1}{r'^2}+ \frac{r'}{c} \frac{d}{dt} \Big( \frac{1}{r'^2} \Big) \ \Big{]} e_{r'} = - \frac{q}{4 \pi \epsilon_0 r'^2} \Big{[} \ 1 \pm \frac{2v}{c} \ \Big{]} e_{r'}$$

The sign depends on position of two points on the line. But this is not the point...

This formula seems definitely wrong. The correct formula must have factor $1 \pm \frac{v}{c}$. On the other hand there is no such corrections in an errata.

Questions

1. Is it my mistake (when I substitute) or mistake in textbook?

2. If it is mistake in textbook, what is correct formula? Where can I find it?

Answer 1

Hint :

Your mistake is this \begin{equation} \dfrac{\mathrm dr'}{\mathrm dt}=\boldsymbol{\pm}\,\upsilon \tag{01-wrong} \end{equation}

The correct one is \begin{equation} \dfrac{\mathrm dr'}{\mathrm dt}= \begin{cases} \dfrac{\upsilon}{\dfrac{\upsilon}{c}-1} & \text{for charge }q \text{ to the left of the field point } \mathrm P\\ \\ \dfrac{\upsilon}{\dfrac{\upsilon}{c}+1} & \text{for charge }q \text{ to the right of the field point } \mathrm P \end{cases} \tag{02-right} \end{equation} where $\:\upsilon(>0)\:$ the speed of the charge towards the positives of the $\:x-$axis (the velocity being $\:\boldsymbol{\upsilon}=\upsilon\, \mathbf{i}\:$ where $\:\mathbf{i}\:$ the unit vector on the $\:x-$axis).

Note that \begin{equation} \mathbf{e}_{r^{'}}= \begin{cases} -\mathbf{i} & \text{for charge }q \text{ to the left of the field point } \mathrm P\\ \\ \hphantom{-}\mathbf{i} & \text{for charge }q \text{ to the right of the field point } \mathrm P \end{cases} \tag{03} \end{equation} and \begin{equation} 1-\dfrac{2\, \mathrm dr'}{c\,\mathrm dt}=\dfrac{c\pm\upsilon}{c\mp\upsilon}= \begin{cases} \dfrac{c+\upsilon}{c-\upsilon} & \text{for charge }q \text{ to the left of the field point } \mathrm P\\ \\ \dfrac{c-\upsilon}{c+\upsilon} & \text{for charge }q \text{ to the right of the field point } \mathrm P \end{cases} \tag{04} \end{equation}

Video here : Electric field of a uniformly moving point charge