Up and down quark content of neutral pion

Question

If isospin were a perfect symmetry, then the neutral pion would have equal $u\bar u$ and $d\bar d$ content, but since up quarks are slightly lighter than down quarks, the neutral pion, being the lightest neutral meson, should have a slightly higher proportion of $u\bar u$ than of $d\bar d$. What does experiment have to say about this? Is pion-neutron scattering (perhaps using deuterium targets) measurably different from pion-proton scattering?

Answer 1

The initial valence quark assignment for the neutral pion came from the quark model, but the best direct experimental constraint on the quark content of the $\pi^0$ probably comes from its measured two-photon decay rate, which limits deviations from $(u\bar{u} - d\bar{d})/\sqrt2$ to not more than a few percent. Pion-nucleon scattering data could be relevant, but the best source of additional information on the valence (and non-valence) quark content of the neutral pion probably comes from electromagnetic multibody decays and scattering.

Quark content of pseudoscalar mesons

The valence quark content of hadrons is primarily determined by fitting their mass, spin, parity, charge parity, flavour, and decay properties into the quark model.

Any physical pseudoscalar meson is going to be a mixture of possible QCD pseudoscalar states. Heavy $c\bar{c}$, $b\bar{b}$, and glueball) states are too massive to measurably contribute, so we expect the lightest neutral pseudoscalar mesons ($\pi^0$, eta and eta-prime) to each be a mixture of the possible $u\bar{u}$, $d\bar{d}$, and $s\bar{s}$ pseudoscalar states:$$ \begin{align} \lvert P_3 \rangle & = \frac{1}{\sqrt{2}}\left( \lvert u\bar{u} \rangle - \lvert d\bar{d} \rangle \right) \\ \lvert P_0 \rangle & = \frac{1}{\sqrt{3}}\left( \lvert u\bar{u} \rangle +\lvert d\bar{d} \rangle + \lvert s\bar{s} \rangle \right) \\ \lvert P_8 \rangle & = \frac{1}{\sqrt{6}}\left( \lvert u\bar{u} \rangle +\lvert d\bar{d} \rangle - 2\lvert s\bar{s} \rangle \right) \\ \end{align} $$

In particular, we expect the neutral pion to be

$$\lvert \pi_0 \rangle = \lvert P_3 \rangle + \left(\frac{\epsilon_1}{\sqrt{3}}+\epsilon_2 \cos{\theta_{ps}}\right)\lvert P_3 \rangle + \left(\epsilon_1\sqrt{\frac{2}{3}} - \epsilon_2 \sin{\theta_{ps}}\right)\lvert P_0 \rangle$$

where $\epsilon_1$, $\epsilon_2$, and $\theta_{ps}$ are mixing parameters. In terms of $u\bar{u}$, $d\bar{d}$, and $s\bar{s}$ states, a possible parameterization is

$$\lvert \pi_0 \rangle = \frac{1}{\sqrt{2}}(1+a)\lvert \bar{u}u \rangle - \frac{1}{\sqrt{2}}(1-a) \lvert \bar{d}d \rangle - \sqrt{2} a \lvert \bar{s}s \rangle$$

The parameter $a$ (and $\epsilon_1$, $\epsilon_2$) should be very small because the strange quark $(m_s\sim 100\, \mathrm{MeV/c^2})$ is similar in mass to the neutral pion $(m_{\pi^0}=135\, \mathrm{MeV/c^2})$ and is so much more massive than up and down quarks ($m_u\sim 2$, $m_d\sim 5\, \mathrm{MeV/c^2}$). The isospin symmetry breaking is expected to be of order

$$a \sim \frac{m_d-m_u}{m_s}\sim \mathrm{ a\,few\,percent}$$

Limit from neutral pion two-photon decays

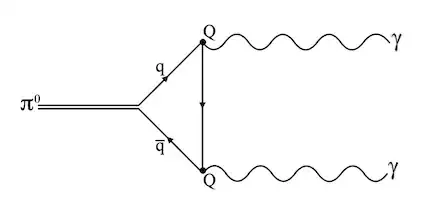
The lowest order process for $\pi^0\rightarrow\gamma\gamma$ decays is this chiral anomaly diagram:

There is a factor of the quark electric charge ($Q$) at each photon coupling vertex, so the two-photon decay amplitude is proportional to $Q^2$ and and hence the decay rate (amplitude squared) should scale as $Q^4$.

For massless up and down quarks, the two-photon decay width of a pure $(u\bar{u} - d\bar{d})/\sqrt2$ pseudoscalar neutral pion can actually be precisely calculated without any free parameters: $$ \Gamma(\pi^0\rightarrow\gamma\gamma) = \frac{m^3_{\pi^0} \; (2S)^2 \alpha^2 \; N_c^2}{64 \pi^3 F^2_{pi^0}} = 7.750 \pm 0.016\,\mathrm{eV} $$ where (following Adler) $S=(Q_u^2-Q_d^2)/2=1/6$ is the quark charge factor for a pure $(u\bar{u} - d\bar{d})/\sqrt2$ state, $\alpha$ is the fine structure constant, $N_c$ is the number of colours, and $F_{pi^0}=92.277\pm0.095$ MeV is the decay constant measured from charged pion weak decays.

The question suggests that because $m_d>m_u>0$, we might expect the pion to have more $\lvert \bar{u}u \rangle$ than $\lvert \bar{d}d \rangle$, which would increase the decay rate because the electric charge of $u$ quarks is 4 times that of $d$ quarks. This naive argument is consistent with more rigorous theoretical calculations that that predicted that the neutral pion decay rate would be 4-5% greater than the chiral anomaly prediction. It was therefore a bit surprising that the best current experimental measurement:

$$ \Gamma(\pi^0\rightarrow\gamma\gamma) = 7.802\pm 0.052(\mathrm{stat.})\pm 0.105(\mathrm{stat.})\,\mathrm{eV} $$

agreed so well with the simple isospin conserving value. This prompted newer theoretical calculations which added next-to-leading-order (NLO) terms that brought theory back into close agreement with the data.

Given that theory and experiment agree with less than 2% uncertainty, the neutral pion quark cannot differ from a pure $(u\bar{u} - d\bar{d})/\sqrt2$ state by more than a few percent.

• Note: The questioner strongly hinted at this themself in their later question on pi-eta-eta' mixing which noted that a "hypothetical $u\bar{u}$ meson should decay to two photons 3.55 times faster than an ideal $(u\bar{u}-u\bar{u})/\sqrt{2}$ meson of similar mass".

Other ways to probe neutral pion quark content

For nucleons, more information about their internal structure is provided by neutrino and electron deep inelastic scattering. The $\pi^0$ is too short-lived for such direct measurements, but indirect probes are possible.

As suggested in the question, one could try comparing pion-neutron and pion-proton scattering, but hadronic physics is messy. Stephen Weinberg noted in 1977 that the mass difference between up and down quarks could produce large isospin violation in pion-nucleon scattering when a least one neutral pion is involved. The neutral pion scattering length can be extracted from $\pi N$ scattering data and pionic atoms, but better data is needed, and it is unclear to me how the effect of any isospin-breaking within the neutral pion could be disentangled from the proton-neutron isospin-breaking.

Instead of hadronic scattering, electromagnetic processes are better tests of the neutral pion's quark content:

• The fact that the strongly kinematically favoured $\phi (s\bar{s}) \rightarrow \pi^0 \gamma$ decay rate is an order of magnitude smaller than the $\phi\rightarrow\eta \gamma$ rate confirms that the $\pi^0$'s valence $s\bar{s}$ content must be very small.

• $e^+e^- \rightarrow e^+e^- \pi^0$ – can determine pion-photon transition form factors, but the experiments are challenging, e.g. Belle and Babar experimental results are not completely consistent.

• $\pi^0 \rightarrow e^+e^- \gamma$ (Dalitz decays) – was used for a "Neutral pion form factor measurement by the NA62 experiment".

• $e^- N \rightarrow e^- N \pi^0$ – is proposed for a "Precision Measurement of the Neutral Pion Transition Form Factor" at Jefferson Lab.

All these measurements are consistent with the neutral pion being a pure $(u\bar{u} - d\bar{d})/\sqrt2$ valence state, but are most interesting because they give information on the form factors that parameterize the distribution of electric charges within the neutral pion, which depends on distributions of both the valence and sea quarks within the neutral pion.