10

In an LC circuit, or an LC tank, the capacitor discharges in one direction through an inductor and then the inductor seems to carry energy in the form of a magnetic field , to charge the capacitor again with current in the same direction.

While it is clear to me why a magnetic field would create that energy when it is "collapsing" into current, i don't understand how is this situation possible, since it seems like the energy coming from the capacitor when it's discharging, somehow doubles itself to charge the capacitor again with the same amount of energy , in the other direction.

I am of course deliberately ignoring the resistance, and assuming it to be zero, just to isolate and understand the functionality better.

And so, there seems to be an extra energy generated by the inductor.

How is it possible for the energy to be used twice? once in the discharge and again in the charging in the other direction. where does this extra energy come from ?

Qmechanic
  • 220,844
physicsnewbie
  • 607
  • 5
  • 10

4 Answers4

20

The energy is not used up. It goes to the magnetic field, and when the magnetic field is at its strongest value there is no energy left in the electric field of the capacitor. But then the magnetic field starts decreasing as the capacitor charges back up because the current starts decreasing. And when the capacitor is fully charged there is no current and no magnetic field.

The whole situation is like a pendulum swinging back and forth. When all the gravitational energy is gone, the pendulum is at its lowest point and has its max kinetic energy. When the pendulum reaches the other side and the gravitational energy "charges back up" you probably recognize there is no doubling of energy because the kinetic energy is gone.

octonion
  • 9,072
12

It depends as to whether you are considering the LC(R) circuit in isolation or with a alternating voltage supply as the driver.

The series of diagrams illustrate what might happen if the capacitor is initially charged and then connected to an inductor (with resistance).

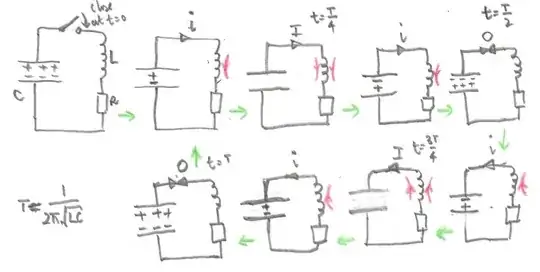
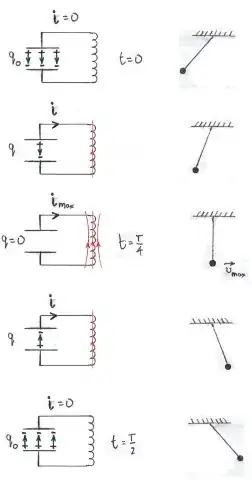
enter image description here

So what is happening is essential an exchange of energy associated with a magnetic field iin the inductor and an electric field in the capacitor.
The mechanical analogue would be a simple pendulum with the kinetic energy associated with the mass of the bob (inductor in LC circuit - magnetic field) and the potential energy associated with the height of the bob (capacitance in LC circuit - electric field).
In the top middle diagram the current in the circuit is a maximum the charges carry on moving (they have inertia) even though there is no change on the capacitor.

The parallel with the motion of a simple pendulum is shown below.

enter image description here

The system undergoes damped simple harmonic motion and the amount the damping being related to the resistance in the circuit.
So with a comparatively small amount of resistance in the circuit the motion of the charges will be under damped or oscillatory and with a lot of resistance the motion of the charges will be over damped.
Because there are unbound accelerating charges the circuit will also produce electromagnetic waves and this will contribute to the damping of the circuit and is characterized by a parameter called radiation resistance.

So energy is conserved and oscillates between one form and another.

If the circuit is connected to an alternating voltage source then it will exhibit all the characteristics of forced oscillations including resonance.
In this case after the transient oscillations have died down the peak current which reach a constant value and any energy dissipated in the resistor will be equal to the energy provided by the voltage source.

Farcher
  • 104,498
4

How is it possible for the energy to be used twice? once in the discharge and again in the charging in the other direction. where does this extra energy come from?

Think of the canonical mass-spring system

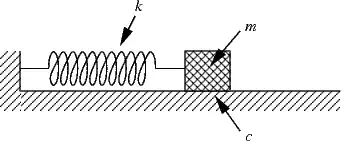
enter image description here

Image credit

Imagine that the mass is pulled to the right some distance $d$ from the equilibrium point and released. The mass oscillates back and forth forever (ideally), passing through the equilibrium point with maximum speed $v_0$ and turning around at a distance $d$ to the left or right.

At the equilibrium point, all of the energy of the system is in the form of kinetic energy $E = \frac{1}{2}mv_0^2$ whether the mass is moving left-to-right or right-to-left.

At a turning point, all of the energy of the system is in the form of potential energy $ = \frac{1}{2}kd^2$ whether the spring is compressed (left turning point) or stretched (right turning point).

Further, the total energy of the system is constant with time since there is no friction (or other dissipation mechanism) by stipulation and so

$$\frac{1}{2}mv_0^2 = \frac{1}{2}kd^2 $$

That is, the energy isn't 'used', it simply 'sloshes' back and forth between potential and kinetic forms.

If the above isn't clear, then stop reading here.

But this is essentially an analog for the LC system where

  • the mass plays the role of the inductor
  • the spring plays the role of the capacitor
  • the force plays the role of the voltage across
  • the velocity plays the role of the current through

At a turning point, the velocity (current through) is zero, the force (voltage across) is maximum and the potential (electric) energy is maximum: $\frac{1}{2}kd^2\, (\frac{1}{2}CV^2)$. But note that the force (voltage across) can be either direction (polarity).

Similarly, at the equilibrium point, the force (voltage across) is zero, the velocity (current through) is maximum, and the kinetic (magnetic) energy is maximum: $\frac{1}{2}mv_0^2\, (\frac{1}{2}LI^2)$. But note that the velocity (current through) can be either direction.

Alfred Centauri
  • 60,633
1

Let me start by emphatically stating that there is no "extra" energy coming into a "pure" LC circuit (other than the starting energy)! Your confusion appears to come from your incomplete understanding of energy, charge, electric and magnetic fields.

When a capacitor is charged, an electric field is created by the charge on the plates (regardless of the polarity).
When current flows through an inductor, a magnetic field is created by the current (regardless of the direction).
Energy is contained in the electric or magnetic field, not on the charge or the current.

When a charged capacitor is connected to an inductor, the charge creates a current, which discharges the capacitor, which "collapses" the electric field, and creates a magnetic field on the inductor.
This sequence of events result in the transfer of energy of the electric field to the magnetic field!

When the current stops flowing, the inductor's magnetic field collapses and induces a current, which creates a voltage, which charges the capacitor, which creates an electric field between the plates of the capacitor.
This sequence of events result in the transfer of energy of the magnetic field to the electric field.

In the absence of resistance, the energy "moves" from the capacitor to the inductor and back, indefinitely!

Guill
  • 2,573