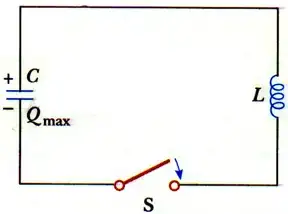
Suppose we have a fully charged capacitor and we connect it to an inductor.
Capacitor will discharge. Inductor will get the current from the capacitor. Wave form of the current shows that the current is oscillating.
It means that the current rises intially. But what makes me confuse is that when capacitor will discharge its voltage will become lesser and lesser and it causes decrease in current in the circuit. While at the same time the inductor voltage(opposite to capacitor voltage) also becomes lesser and lesser and it cause more current to flow in the circuit.
So less capacitor voltage makes the current less and less inductor voltage cause more current at the same time. Then what makes sure that current will initially rise and will then fall during the first half cycle of the oscillation ?