Bra Ket Notation and Derivative

Question

Let $$a$$ be the partial derivative symbol with respect to $x$. What is $$\langle x|a|x \rangle$$ equal to? I think it is 0 but not sure.

Answer 1

As answered in the questions linked in the comments, the correct thing to look for is $\langle x | a | x'\rangle=\delta'(x-x')$. I guess for your calculation $\langle x|a|x\rangle=\delta'(0)=0$ (we have $\delta'(-x)=-\delta'(x)$, so it must be an odd function. So if it has any well-defined value at zero [which it doesn't!] it has to be zero. Trimok gives a similar answer here).

Let's check this: We should have $\psi'(x)=\langle x | a | \psi\rangle$ by the definition of $a$. But we should also be able to insert identity $1=\int |x'\rangle\langle x'| \text{d}x'$ anywhere we like, so that $\psi'(x)=\int \text{d}x'\langle x | a |x'\rangle\langle x' | \psi\rangle$. Hence $\psi'(x)=\int \text{d}x'\langle x | a |x'\rangle \psi(x')$ for all $\psi$. If we plug in $\langle x | a | x'\rangle=\delta'(x-x')$, then we get the integral $\int \text{d}x'\delta'(x-x') \psi(x')$. This can be integrated by parts: \begin{align*} (\cdots)&=-\int \psi(x')\text{d}\left(\delta'(x-x')\right) \\ &=\int \psi'(x')\delta(x-x') \text{d}x'\\ &=\psi'(x) \end{align*}

So our formula is correct!

See also derivations of the same thing (divide through by $-i\hbar$ to get my formula) as answers here and here.

Answer 2

I think you are confusing two concepts.

When you have a quantum state and represent it by a ket, $| \psi \rangle$, you are using linear algebra as your formalism. The evolution of such state can be done with linear operators. These operators can be represented as matrices when your space has finite dimensions.

However, there is another way to see quantum mechanics: using functions. Your state could be represented by a continuous function $\psi(x)$, and then you are using calculus as your mathematical formalism. Then, the operators are simply things that act over these functions, such as the derivatives.

What is the relationship between the two points of view? I will not go into mathematical details, but it is possible relate both views using

$$\langle x | \psi \rangle = \psi(x)$$

This is called position representation. You can have more, for example, momentum representation, $\langle p | \psi \rangle = \psi(p)$, where $\psi(p)$ is the Fourier transform of $\psi(x)$.

So, you have two ways of seeing the operators. For example, $\hat p$, the momentum operator, can act over any state $| \psi \rangle$, as you usually do in linear algebra.

But you could also use space representation:

$$\langle x | \hat p | \psi \rangle = -i\hbar\frac{\partial}{\partial x}\psi(x)$$

This is the reason why you identify $\hat p\equiv -i\hbar\frac{\partial}{\partial x}$. However, rigurously speaking, this is what you obtain from the momentum operator in position representation.

So, you can do it also using, for example, momentum representation:

$$\langle p |\hat p| \psi \rangle = p\psi(p)$$

In this case, since $ | p \rangle $ is an eigenstate of the momentum operator, you have $\hat p | p \rangle = p | p \rangle$ and it is simply multiplying by $p$. You see that if you Fourier transform your function then there is no derivative at all when applying the momentum operator.

So, I think that you see now that writing something like

$$ \langle x | \frac{\partial}{\partial x}| \psi \rangle $$

simply makes no sense. (see disclaimer below). You are mixing the two different ways to view QM. So you can use linear algebra or functions. You can switch between them as you want using your favorite representation. But you should not mix the things.

I know I have been a bit lossy mathematically, but I hope this will make easier to understand.

EDIT: after some comments (and a pair of downvotes), I think that I have to add some disclaimer. In fact, a vector in a Hilbert space can depend on some variable, for example, a state can vary in time: $| \psi(t) \rangle$. Then, if the basis we are using the represent the vectors is fixed, the following notation is usual:

$$ | \psi(t) \rangle = \sum _{n=0} ^{+\infty} c_n(t) | e \rangle$$ $$\frac{\partial}{\partial t} | \psi(t) \rangle \equiv \sum _{n=0} ^{+\infty} \frac{\partial c_n(t) }{\partial t} | e \rangle$$

However, the derivative of the left hand side of the equal acts over a vector and gives another vector in the Hilbert space. And in the right side, we have the normal derivative over functions. They have different domains, so they are different things. My answer simply focus in the difference between the derivative as an operator in the Hilbert space and in the space of functions. Maybe it is clearer now. Hope I didn't make a mess with this. Please tell me if I am wrong.

Answer 3

Well, from a clean mathematical point of view, the "object" $\langle x | \frac{\partial}{\partial x}| x\rangle$ is totally nonsensical, even judging by Dirac's liberal view of using a mambo-jumbo mixture of ill-defined mathematical expressions. In the standard (Dirac-like) mathematical interpretation of the bra-ket formalism of Quantum Mechanics (cf. quant-ph/0502053 v1) we have:

• $\langle x |$ is the solution of the spectral equation for the dual-position operator $x'$ in 1D (unbounded motion, i.e. $\sigma(x)=\mathbb{R}$) in the abstract space $\Phi'$ of a nuclear rigging $\Phi\subset \mathcal{H}\subset \Phi'$ of a complex infinite dimensional Hilbert space $\mathcal{H}$ in which the Born-Jordan CCRs problem $[x,p] \subset i\hbar 1_{\mathcal{H}}$ is well-posed in the sense of Stone-von Neumann-Rellich-Dixmier.
• $|x\rangle $ is the solution of the same problem, but with the anti-dual operator $x^\times$ and $\Phi^\times$ the topological anti-dual of $\Phi$.

The fact that these two objects are elements from different spaces is not so troubling, one can essentially identify them by their action on the same vector $\phi\in\Phi$. They are topologically the same, no matter what topologization is used. The only trouble is that the operator $\partial_x$ already uses the so-called realization of the abstract RHS $\Phi\subset \mathcal{H}\subset \Phi'$ by a set of functions and distributions, so this operator, either acting to the right, or acting to the left of the Dirac expression $\langle x | \frac{\partial}{\partial x}| x\rangle$ is simply not defined.

The realization of an abstract RHS by a set of (equivalence classes of) functions and distributions is done only at formal level, by defining formal objects such as $\langle x |p\rangle$ (formality here means there is no way to combine the bra and the ket defined separately as above to obtain a true tempered distribution):

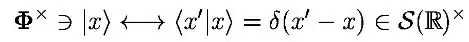Without this realization, there's really no way to conceive extending the partial derivative operator from $\Phi$ to $\Phi'$ or $\Phi^\times$, because, as explained, it doesn't act on the space of the bra's and the ket's.