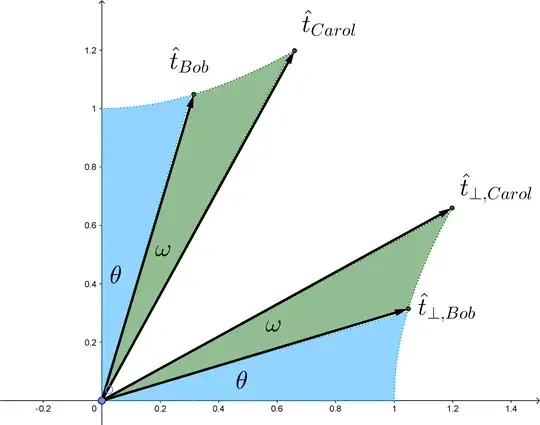
Under a boost by relative-spatial-velocity $w=v_{CB}=\tanh\omega$,
Bob's 4-velocity vector is transformed into Carol's 4-velocity vector.
Call $\omega$ the relative-rapidity between the [timelike] 4-velocities.
The [spatial-]velocity transformation
$$v_{CA}=\frac{v_{BA}+v_{CB}}{1+v_{BA}v_{CB}}$$
provides her spatial-velocity [the slope of Carol's 4-velocity vector] $v'=v_{CA}=\tanh(\theta+\omega)$
in terms of the Bob's spatial-velocity $v=v_{BA}=\tanh\theta$ and the relative spatial velocity $w=v_{CB}=\tanh\omega$.
That boost also transforms
Bob's "space axis" [with slope $1/v_{BA}$] into Carol's "space axis" [with slope $1/v_{CA}$]. (This is true because, in Minkowski spacetime geometry, two directions are perpendicular in that geometry when the product of the slopes is +1... to be contrasted with the Euclidean case where the product is $-1$. Note that by taking the product of the two formulas in the OP the right side simplifies.)
Although, technically speaking, the angle between spacelike lines isn't the rapidity... these spacelike lines are special because they are correspondingly perpendicular to the 4-velocities in the problem (that of Alice [not shown] and of Bob and Carol) and coplanar with all of them.
UPDATE:
Here is an algebraic calculation to support the spacetime diagram above.
I use signature $(+,-)$, where my first component is the time component.
Let $\hat V=\left(\begin{array}{c} \cosh{B} \\ \sinh{B} \end{array}\right)$ be Bob's 4-velocity (a timelike vector).
His spatial velocity $v=\rm{slope}=\frac{\rm spatial\ component}{\rm temporal\ component}=\frac{\sinh B}{\cosh B}=\tanh{B}$.
Let $M=\gamma\left(\begin{array}{cc} 1 & \beta \\ \beta & 1 \end{array}\right)$ be a boost that maps Bob's 4-vector to Carol's 4-vector.
(The boost velocity $\beta$ corresponds to $w$ in the OP.)
I am intentionally mixing notations to distinguish the boost components from the 4-velocity components.
So, we get Carol's 4-velocity
\begin{align}
\hat V'&=M\hat V\\
\hat V'&=
\gamma\left(\begin{array}{cc} 1 & \beta \\ \beta & 1 \end{array}\right)
\left(\begin{array}{c} \cosh{B} \\ \sinh{B} \end{array}\right)\\
&=
\gamma\left(\begin{array}{c} \cosh{B} + \beta\sinh{B} \\ \beta\cosh{B}+\sinh{B} \end{array}\right) = \left(\begin{array}{c} \cosh{C} \\ \sinh{C} \end{array}\right)\\
\end{align}
$\hat V'$ has slope $$v'=\tanh{C}=\frac{\beta\cosh{B}+\sinh{B}}{\cosh{B} + \beta\sinh{B}}
=\frac{\beta+\tanh{B}}{1+\beta\tanh{B}}=\frac{\beta+v}{1+\beta v},$$
the velocity transformation (the OP's eq. 1).
Next...
Let $\hat V_{\perp}=\left(\begin{array}{c} \sinh{B} \\ \cosh{B} \end{array}\right)$ be Bob's unit-x vector (a spacelike vector orthogonal to his 4-velocity $\hat V$). It has slope $v_{\perp}=\frac{\cosh B}{\sinh B}=\coth B=\frac{1}{v}$.
The boost will map this vector to Carol's unit-x vector $\hat V_{\perp}'$ (a spacelike vector orthogonal to Carol's 4-velocity $\hat V'$).
So,
\begin{align}
\hat V_{\perp}'&=M\hat V_{\perp}\\
\hat V_{\perp}'&=
\gamma\left(\begin{array}{cc} 1 & \beta \\ \beta & 1 \end{array}\right)
\left(\begin{array}{c} \sinh{B} \\ \cosh{B} \end{array}\right)\\
&=
\gamma\left(\begin{array}{c} \sinh{B} + \beta\cosh{B} \\ \beta\sinh{B}+\cosh{B} \end{array}\right)
\end{align}
$\hat V_{\perp}'$ has slope $$v_{\perp}'=\frac{\beta\sinh{B}+\cosh{B}}{\sinh{B} + \beta\cosh{B}}
=\frac{\beta+\coth{B}}{1+\beta\coth{B}}=\frac{\beta+v_{\perp}}{1+\beta v_{\perp}}=\frac{\beta+(\frac{1}{v})}{1+\beta (\frac{1}{v})},$$
call it the spacelike-slope transformation (the OP's eq. 2).
For completeness, we should show that $v_{\perp}'=\frac{1}{v'}$.
\begin{align}
v_{\perp}'
&\stackrel{?}{=}\frac{1}{v'}\\
&\stackrel{?}{=}\frac{1+\beta v}{\beta + v}\\
&\stackrel{\surd}{=}\frac{(\frac{1}{v})+\beta }{\beta (\frac{1}{v}) +1}\\
\end{align}
...and we are done.
In my opinion, the PHYSICAL interpretation is that it is the slope of the observer's X-axis. (One can probably find other interpretations... but at the root of it... it is this slope.)
UPDATE #2 (in response to the OP's update and comments):
In a Lorentz boost, we can see how the 4-velocity and spatial-axis of an observer transform in a complementary way by viewing a "light-clock diamond" on "rotated graph paper".
This is taken from a blog entry I contributed to at
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/
This is based on my recent paper (“Relativity on Rotated Graph Paper”, Am. J. Phys. 84, 344 (2016); http://dx.doi.org/10.1119/1.4943251 ).
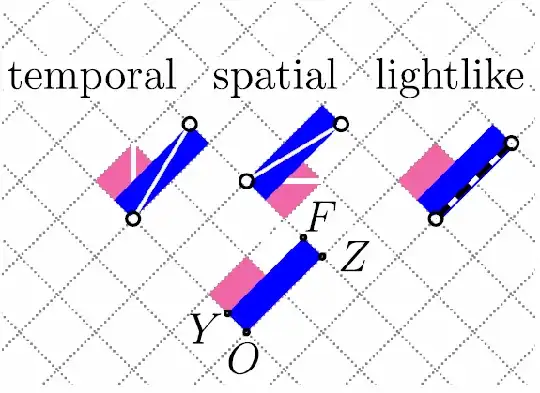
On these diagrams, time runs upwards.
Light-Clock Diamonds are traced out by the spacetime paths of light-signals in a longitudinal light-clock. The worldlines of the mirrors of the light-clock are not shown, but are implied by the reflection events. In each tick of the light-clock, these events are "spatial" according to the observer carrying that light-clock. That is, that direction is Minkowski-perpendicular to that observer's 4-velocity. Visually, this means that the diagonals of a light-clock diamond are Minkowski-perpendicular to each other.
Under a boost, Alice's light-clock diamond must transform into Bob's light-clock diamond, which must have edges parallel to the light-cone (to preserve the speed of light) and must have area preserved (since the Lorentz boost has determinant equal to one). [The area turns out to be the square-interval of OF.]
Geometrically, the tip of the 4-velocity travels along the unit-hyperbola centered at the origin. [This ensures that the area of the diamond is preserved]. At the intersection point, the tangent to the hyperbola is Minkowski-perpendicular to the 4-velocity [a unit radius vector]. This tangent is parallel to the spacelike-diagonal of the light-clock diamond.
Thus, diagonal YZ is Minkowski-perpendicular to diagonal OF.