Why are $L_4$ and $L_5$ lagrangian points stable?

Question

This diagram from wikipedia shows the gravitational potential energy of the sun-earth two body system, and demonstrates clearly the semi-stability of the $L_1$, $L_2$, and $L_3$ lagrangian points. The blue arrows indicate lower potential energy, red higher - so any movement in the plane perpendicular to the masses would require energy and without it, an object there would settle.

However, the $L_4$ and $L_5$ are claimed to be stable, even though the direction arrows indicate it's at the top of a gravity well, and would fall into lower potential energy in any direction. What is it that makes these points stable if not gravity? What am I missing?

Answer 1

When you look at the dynamics in the rotating reference frame, there are 4 forces acting on the particle: the two gravitational pulls from the massive bodies, the centrifugal push away from the center of rotation (located between the massive objects) and the Coriolis force.

The first three forces depend on the position of the particle, and can be derived from a potential (that also depends on the position), whose level curves are shown in the picture presented with the question. This potential has local maxima at L4 and L5.

The Coriolis force depends on the velocity of the particle: it is perpendicular to it, contained in the plane of motion and proportional to the speed. It curves the motion of the particle to the right (if the massive bodies and the reference system rotate counterclockwise, which is what you see in our Solar System if you stand on the North pole of the Earth).

If a particle placed at L4 tries to leave the point with a mild speed, the Coriolis force curves its trajectory. The trajectory is too curly to get anywhere. See the animation at http://demonstrations.wolfram.com/OrbitsAroundTheLagrangePointL4/.

Of course this doesn't prove that the particle will stay near L4 forever. I don't know a proof. I've seen some computations that show that the dynamical equation linearised at L4 is stable if the mass ratio of the massive objects is sufficiently large, but this also is not enough to prove stability in the non-linearised problem.

I would be convinced that the equilibrium is stable if I were shown that there exists a conserved quantity (depending on the position and speed) that has a strict local extremum at that point of phase space (position=L4, speed=0).

The "energy" (potential discussed above + kinetic energy measured in our non-inertial reference system) is conserved, because the Coriolis force is perpendicular to the trajectory, so it doesn't perform work (in fact, in Lagrangian mechanics it is derived from a potential that depends on the position and speed of the particle). But this quantity doesn't have an extremum at our equilibrium point, because the potential has a local maximum at L4 and the kinetic term is minimum when the speed is 0.

So I can't prove that the equilibrium is stable.

Answer 2

Here's another way of looking at it. Let $M_1$, $M_2$, $M_3$ be our three masses. In the three body problem we're considering, the whole frame containing $M_1$, $M_2$ and $M_3$ is rotating.

You're right to think that if that frame was fixed then the points L4 and L5 would not be stable. After all if you perturb $M_3$ from L4 or L5 then it should just roll down the potential hill.

But there is another force at work here. Because the frame is rotating there is a fictitious force called the Coriolis force which you would feel. This is the same force that makes hurricanes rotate into spirals when seen from space.

When you take the Coriolis force into account, L4 and L5 become stable fixed points. That is, if you perturb $M_3$ from L4 a little bit it will just stay at it's perturbed distance and orbit the point L4.

If anyone wants to see the maths for this then check out this useful article.

Answer 3

As others have commented, including OP, the effective potential (consisting of gravity & the centrifugal potential) $$V~=~ -\frac{Gm_1}{|z_1|} - \frac{Gm_2}{|z_2|} -\frac{\Omega^2 |z|^2}{2} \tag{1} $$ in the orbital plane $\mathbb{R}^2\cong\mathbb{C}$ has a global maximum at the Lagrange points $L_4$ and $L_5$, $$\begin{align}z_1~=~&\hspace{5mm} R\exp\left\{\pm \frac{i\pi}{3} \right\} ~=~\hspace{5mm}\frac{R}{2}\pm\frac{\sqrt{3}iR}{2}, \cr z_2~=~&-R\exp\left\{\mp \frac{i\pi}{3} \right\}~=~-\frac{R}{2}\pm\frac{\sqrt{3}iR}{2} .\end{align} \tag{2}$$ I'm here using the same notation as my Phys.SE answer here: $$\begin{align}z_1~:=&~ z-r_1~\neq~0,\cr z_2~:=&~ z-r_2~\neq~0,\cr \Omega^2~:=&~\frac{G(m_1+m_2)}{R^3}.\end{align} \tag{3}$$ Usually a test particle doesn't want to be at a global maximum! However, we should not forget the Coriolis force.

Main statement. When the test particle tries to leave $L_4$ or $L_5$, the Coriolis force will prevent this via deflection iff one of the mass ratios $m_1/m_2$ or $m_2/m_1$ exceeds $$\frac{25}{2}+\frac{3}{2}\sqrt{69}~\approx~25.\tag{4}$$

In this answer, I would like to calculate this mass ratio condition (4), which is also mentioned on Wikipedia.

The Hessian of the effective potential (1) is $$ \begin{align}H^{ik}~:=~&\frac{\partial^2 V}{\partial z^i \partial z^k},\qquad i,k~\in~\{1,2\},\qquad {\bf z}~\in~\mathbb{R}^2,\cr {\bf H}~=~& -Gm_1 \left(\frac{3{\bf z}_1{\bf z}_1^T}{|{\bf z}_1|^5}-\frac{{\bf 1}_{2\times 2}}{|{\bf z}_1|^3}\right)\cr &-Gm_2 \left(\frac{3{\bf z}_2{\bf z}_2^T}{|{\bf z}_2|^5}-\frac{{\bf 1}_{2\times 2}}{|{\bf z}_2|^3}\right) -\Omega^2{\bf 1}_{2\times 2} . \end{align} \tag{5}$$ At $L_4$ or $L_5$, the Hessian becomes $$\begin{align} {\bf H}~=~&-\frac{3\Omega^2}{4} \begin{pmatrix} 1 & \pm \sqrt{3}\epsilon_{12} \cr \pm \sqrt{3}\epsilon_{12} & 3 \end{pmatrix}, \cr \epsilon_{12}~:=~&\epsilon_1-\epsilon_2~=~\frac{m_1-m_2}{m_1+m_2}~=~1-2\epsilon_2~\in~]-\!1,1[. \end{align} \tag{6}$$ The trace & determinant are $$ {\rm tr}({\bf H})~=~-3\Omega^2 \qquad\text{and}\qquad \det({\bf H})~=~\frac{27\Omega^4}{16}(1-\epsilon^2_{12})~>~0. \tag{7}$$

We now use the following theorem$^1$ mentioned in Ref. 1:

Theorem. Let there be given a Hessian ${\bf H}$ for an effective potential $V:\mathbb{R}^2\to\mathbb{R}$ at a Lagrange point. Let $\Omega$ be the angular velocity. The following 3 conditions are necessary & sufficient conditions for the Lagrange point to be stable:

1. $C~:=~\det({\bf H})~\geq~0. $

2. $B~:=~{\rm tr}({\bf H})+4\Omega^2~\geq~0. $

3. $D~:=~B^2-4C~\geq~0. $

NB: The above theorem ignores higher-order terms in $V$, which could become important if $\det({\bf H})=0$.

The first two conditions are satisfied: $$C~=~\frac{27\Omega^4}{16}(1-\epsilon^2_{12})~>~0 \qquad\text{and}\qquad B~=~\Omega^2~>~0.\tag{8} $$ The third condition reads $$0~<~D~=~\frac{27\epsilon^2_{12}-23}{4}~=~27\left(\epsilon^2_2-\epsilon_2 +\frac{1}{27} \right) \tag{9}. $$ The roots of the quadratic equation $D=0$ are $$ \frac{m_2}{m_1+m_2}~\equiv~\epsilon_2~=~\frac{1}{2} \pm \frac{\sqrt{69}}{18}~\approx~\left\{\begin{array}{c}25/26,\cr 1/26.\end{array}\right.\tag{10}$$ This leads to the condition (4). $\Box$

References:

1. J. Binney & S. Tremaine, Galactic Dynamics, 2nd edition (2008); p. 181-182.

--

$^1$ Proof of theorem: The linearized EOM at a Lagrange point ${\bf z}={\bf 0}$ in the orbital plane $\mathbb{R}^2$ reads

$$\ddot{\bf z} ~\approx~\underbrace{2 \Omega ~{\bf J} \dot{\bf z}}_{\text{Coriolis}} - {\bf H} {\bf z}, \qquad {\bf J}~:=~\begin{pmatrix} 0 & 1 \cr -1 & 0 \end{pmatrix},\tag{11}$$

where the first term on the rhs. is the Coriolis force. The Hessian is a real symmetric matrix, and therefore diagonalizable with 2 principal axes. After a possible coordinate rotation ${\bf z}\mapsto e^{J\phi}{\bf z}$, we may assume that the Hessian

$${\bf H}~=~\begin{pmatrix} H_1 & 0 \cr 0 & H_2 \end{pmatrix}\tag{12}$$

is diagonal. (The rotation commutes with the Coriolis term (11) and leaves the 3 conditions in the theorem invariant!) The EOMs (11) are 2 coupled 2nd-order homogeneous ODEs with constant coefficients. Their characteristic equation is a 4th order equation $$0~=~\left| \begin{array}{cc} \lambda^2 +H_1& -2\Omega \lambda \cr 2\Omega \lambda & \lambda^2 +H_2 \end{array} \right| ~=~(\lambda^2)^2 +B\lambda^2 +C \tag{13},$$ which has 4 roots $$ \lambda^2~=~\frac{-B\pm \sqrt{D}}{2}\tag{14} .$$ Eq. (13) is a 2nd order eq. in $\lambda^2$. The solution to the 2 coordinates $z^1$ and $z^2$ are linear combinations of exponentials $e^{\lambda t}$, where $\lambda$ is a root. The condition of stability is that ${\rm Re}(\lambda)\leq 0$ for all 4 roots.

However due to symmetry in eq. (13), if $\lambda$ is a root, so is $-\lambda$. So the condition of stability is that ${\rm Re}(\lambda)=0$ for all 4 roots, i.e. that $\lambda$ is imaginary. Or equivalently, that $\lambda^2 \leq 0$ is non-positive for all 4 roots.

This is only possible if the discriminant $D\geq 0$ in eq. (14) is non-negative, i.e. the 3rd condition in the theorem.

The 1st & 2nd conditions $$ C,B~\geq~ 0\qquad\Leftrightarrow\qquad\lambda^2_{\pm}~\leq~0 \tag{15}$$ follow from the well-known fact that $$ C~=~ \lambda^2_+\lambda^2_-\qquad\text{and}\qquad-B~=~\lambda^2_++\lambda^2_- \tag{16} $$ in the 2nd order eq. (13) are the product and sum of its roots, respectively. $\Box$

Answer 4

I think there are some good explanations here, but I'll try to add a very simplified, hopefully intuitive explanation.

First, let's agree on some conventions. Suppose the Earth is going counterclockwise around the Sun. It's going in a circular orbit at a distance $R$ (from the barycenter) with angular velocity $\Omega$.

We're going to focus on L4. First suppose you started exactly on L4, moving at just the right speed to stay there. This is certainly an equilibrium that doesn't require any force to maintain - we'll leave the issue of stability alone for a bit. What speed are you going while staying on L4? Well, your angular velocity must simply be the pattern speed $\Omega$, meaning in the corotating frame (the one in which the Sun and Earth are fixed just as pictured) you don't move at all. In the inertial frame with the barycenter of the system at rest, you must have a speed $\Omega R$, and it's directed entirely in the azimuthal direction - that is, tangent to the circle of your orbit.

Now suppose you're displaced from that cozy equilibrium position. For specificity, we'll assume you now find yourself a little bit closer to the barycenter; you were moved along the line connecting it to L4. Also, you didn't lose too much kinetic energy (to be made precise in the next paragraph). This is important. If something, say a viscous drag, keeps draining your total energy, you will have to fall into a lower part of the potential surface, and you won't be able to stay near L4.

Another simplifying assumption: your momentum is still in the same direction as it was when you were blissfully sitting at L4. That is, it is entirely azimuthal. So what's your situation now. Well, your new distance from the barycenter is $R - \Delta R$. To keep up with the pattern speed (i.e., to not be moving with respect to the Earth and L4 in that diagram), you need an azimuthal speed of $\Omega (R - \Delta R) < \Omega R$. You don't need as much speed, and hence you don't need as much kinetic energy, to keep up with the rotation. You originally had a specific kinetic energy (kinetic energy per unit mass) of $(1/2) \Omega^2 R^2$, and now as long as you have more than $(1/2) \Omega^2 (R - \Delta R)^2$, you'll advance ahead of the pattern.

So referring to the figure, you were displaced to somewhere below and to the left of L4, and now you'll be moving up and to the left, at least initially. Just like any test mass with a tangential velocity too great for a circular orbit, you'll be moving outward. In the rotating frame, this could be construed as a manifestation of the Coriolis force. [Aside: The Coriolis force acts in the direction $-\vec{\Omega} \times \vec{v}$, and with $\vec{\Omega}$ pointing up out of the page and $\vec{v}$ (your velocity in the rotating frame) pointing azimuthally counterclockwise, you can see this will cause an outward-directed acceleration.] But this is more obvious in the inertial frame, where you're now going too fast for the Sun's gravity to bend your path into a circle.

So what happens? As you advance ahead of the pattern (your angular velocity is greater than $\Omega$), you also are pushed outward. Eventually you find yourself at a distance $R$ again, but now you're ahead of (counterclockwise of, up and to the left of) L4. The radial "force" will vanish somewhere around here, but remember you have inertia, whether your reference frame is inertial or not! So you'll coast outward, to distances from the barycenter greater than $R$. On this side of $R$, however, everything is reversed. You don't have enough speed to keep up with an angular velocity $\Omega$, so you fall behind. You are now moving counterclockwise in that rotating frame, looping around the outside of L4. Of course, because you're going too slow to keep a circular orbit (described in the inertial frame), or because there's an inward-directed Coriolis force (described in the rotating frame), you're accelerated inward. Eventually you'll move around behind L4 and return somewhere near where you started this journey just after getting displaced.

The orbits can be complicated to describe analytically, but hopefully this shows where the "forces" come into play, and where they're directed. You end up tracing a path that goes clockwise around L4 (note all my other uses of "clockwise"/"counterclockwise" have been with respect to the barycenter).

One final note: In the rotating frame this is truly a dynamics problem, where you can't get the motion just by differentiating a simple potential. Note that we started to do that, and that's what lead to the confusion. In addition to the gravitational potentials induced by the two masses, we added a term to the effective potential (the function whose contours are plotted in the diagram) to take care of centrifugal force: $$ \Phi_\text{eff}(\vec{x}) = -G \left(\frac{M_\odot}{\lvert \vec{x}-\vec{x}_\odot\rvert} + \frac{M_\oplus}{\lvert \vec{x}-\vec{x}_\oplus\rvert} + \frac{M_\odot+M_\oplus}{2\lvert \vec{x}_\oplus-\vec{x}_\odot \rvert^3} \lvert \vec{x} \rvert^2\right), $$ where $\vec{x}$ is the two-dimensional vector in the plane of the system with origin at the barycenter. (Binney & Tremaine's Galactic Dynamics derives this in a roundabout aside; there are probably more direct treatments.) We can only stop here, however, if we only want to consider forces on particles at rest in the rotating frame. As pointed out in another post, the centrifugal force ($-\vec{\Omega} \times \vec{\Omega} \times \vec{x}$) isn't the only fictitious force we have to worry about. If the test object has a velocity with respect to the rotating frame, as in the case at hand, we have the Coriolis force ($-2\vec{\Omega} \times \dot{\vec{x}}$), which we did not account for in setting up the effective potential. The reason is it's not just a function of 2-D position space, but of the whole 4-D phase space. There's one other common fictitious force that fortunately we didn't have to consider: the Euler force ($-\dot{\vec{\Omega}} \times \vec{x}$). This would only come into play if the pattern speed were changing (say if the Earth had some additional acceleration, perhaps from being in an eccentric orbit).

Answer 5

Three topics:

1. There's an electromagnetic analogy for the non-inertial forces in a rotating reference frame.
2. Before looking at the restricted three-body problem of the question, analyze the familiar two-body problem in a rotating reference frame. I think that interpreting these results in terms of the known solutions for this problem is instructive.
3. Finally, look at the Lagrange points.

1. Electromagnetic analogy. It turns out that the non-inertial forces on a mass $m$ in a rotating reference frame can be manipulated into exactly the form of the electromagnetic Lorentz force on a charge $q$ in an inertial frame.

Reference by Moreno and Barrachina (pdf) . There are some unfortunate typos, but I think the results I state are accurate.

Specifically, for a rotating reference frame with angular velocity $\boldsymbol{\omega}$, if the electromagnetic scalar potential $\phi$ and vector potential $\boldsymbol{A}$ are taken to be: $$ \phi = -\left(\frac{m}{q}\right) \frac{\boldsymbol{(\omega \times r)^2}}{2}$$ $$ \boldsymbol{A} = \left(\frac{m}{q}\right) \boldsymbol{\omega \times r} $$ then the electromagnetic force on the charge $q$ in an inertial frame is the same as the non-inertial forces on the mass $m$ in the rotating frame.

In particular, for a constant angular velocity $\boldsymbol{\omega}$ that is perpendicular to the plane of motion (like in this problem), in cylindrical coordinates $(r,\theta,z)$, the analogous electric field $\boldsymbol{E}$ and magnetic field $\boldsymbol{B}$ are: $$E=\left(\frac{m}{q}\right) \omega^2 r \, \, \boldsymbol{\hat{r}}$$ $$B=\left(\frac{m}{q}\right) 2 \omega \boldsymbol{\hat{z}}$$

The electric field "simulates" the centrifugal force, and the magnetic field the Coriolis force. All intuition from the Lorentz force then carries over: the Coriolis force diverts a body perpendicular to its velocity, forming circles in the absence of other forces.

2. Two-body problem in a rotating frame. The two-body problem ($M_s$ (sun), $M_e$ (earth)) can be formulated in a rotating frame with angular velocity $\omega$ (making the angular velocity the independent variable). Performing the usual conversion to a single-body potential $U$, one gets: $$U=-\frac{GM_t M_r}{r} - M_r \frac{\omega^2 r^2}{2} -M_r \omega r^2 \dot{\theta}$$ $$\text{ where } \qquad M_t=M_s+M_e , \qquad \frac{1}{M_r}=\frac{1}{M_s} + \frac{1}{M_e} , \qquad \alpha=\frac{M_e}{M_t}, \beta=\frac{M_s}{M_t} $$

Solving for a stationary point $r_o$ (with $\dot{\theta}=0$), one gets the usual result: $$r_o = \left(\frac{G M_t}{\omega^2} \right)^\frac{1}{3} , \text{sun x-y coordinates }(x_s,y_s)=(-\alpha r_o, 0) , \text{earth }(x_e,y_e)=(\beta r_o, 0)$$

But observe that the potential at $r_o$ is a maximum, not a minimum!

To see what's going on, find the linearized equations of motion around the stationary point. $$(x,y)=(x_o+\delta x,y_o+\delta y) \qquad , \qquad (v_x,v_y) = (\delta v_x, \delta v_y) $$ $$ \frac{d}{dt} \left( \begin{array}{c} \delta x \\ \delta y \\ \delta v_x \\ \delta v_y \end{array} \right) = \left( \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -q_{xx} & -q_{xy} & 0 & 2 \omega \\ -q_{xy} & -q_{yy} & -2 \omega & 0 \end{array} \right) \left( \begin{array}{c} \delta x \\ \delta y \\ \delta v_x \\ \delta v_y \end{array} \right) $$ $$ \text{ with } q_{xx}=\frac{1}{m} \frac{d^2U}{dx^2}, q_{yy}=\frac{1}{m} \frac{d^2U}{dy^2}, \text{ and } q_{xy}=\frac{1}{m} \frac{d^2U}{dx \, dy} $$ The natural frequencies $s_i$ are the roots of the characteristic polynomial, which turns out to be: $$ s^4 - \Gamma s^2 + \Delta = 0$$ $$ \text{ where } \Gamma = -( q_{xx} + q_{yy} +4 \omega^2) \text{ and } \Delta = q_{xx} q_{yy} - q_{xy}^2$$

For this case, only $q_{xx}=-3 \omega^2$ is non-zero (negative curvature at a maximum), so one finds $\Gamma =- \omega^2$ and $\Delta=0$, and the natural frequencies are: $$ s_{1,2} = 0 \qquad , \qquad s_{3,4}=\pm i \omega $$ corresponding to neutral response or oscillatory motion at the rotation frequency. The Coriolis force bends the trajectories and thereby "converts" an unstable equilibrium into a center of oscillatory motion.

Interpretation: A circular orbit (corresponding to the stationary point) is only one possible solution of the two-body problem; in general orbits are ellipses, so one should expect oscillatory motion around the stationary point, periodic at the rotation frequency. (I think the 0 natural frequencies correspond to an azimuthal shift in position.) The point is that the motion is not unstable, despite it being a local maximum, and the lack of damping (negative real part of the natural frequencies) should be expected.

(By the way, if $q_{xx}$ were positive, corresponding to a local minimum, the resulting oscillatory natural frequencies would be at a higher frequency that $\omega$, and the resulting motion would not be elliptical.)

3. Lagrange points The restricted three-body problem can be analyzed in the same fashion as above, and the stability of each stationary point determined. A reference is Cornish (pdf). It turns out that L1, L2, and L3 all have positive real natural frequencies and therefore are unstable. L4 and L5 have all pure imaginary natural frequencies (as long as $M_e<25 M_s$), and therefore have motions similar to that of the two-body problem.

Update: Here are some notes on the character of the dynamics at the various Lagrange points:

L4 & L5: These points are most like the two-body problem, with a relatively small, negative (de-stabilizing) potential curvature that is stabilized by the Coriolis force.

L3: This point (planet "x" on the other side of the sun from the earth) is the most interesting to me. Since the curvatures are again small (like for the earth two body problem), and one of them is in fact positive (stabilizing), it seems odd that L3 is unstable. The resolution is that the opposite-sign curvatures form a saddle point. A body can escape from such a point by traveling slowly near the line of zero curvature (and hence zero force); with the proper angle and velocity it accelerates slowly and the Coriolis force is ineffective at stopping the escape.

L1 & L2: These points are unstable on two counts: a) the large negative (de-stabilizing) potential curvature from the nearby earth overwhelms the stabilizing effect of the Coriolis force and b) the principal curvatures differ in sign (like L3), forming a saddle point.

Answer 6

I'm not sure that there is a simple intuitive explanation, but let's try this:

Before we can clarify the reason for why these point are stable, note the following: if you have an object orbiting around another (to make it simple) much bigger one. This system is isolated an contains a certain total energy. Now if we would like to find other configurations of this two body system with the same energy, we'd find them by decreasing the potential energy (so decreasing the distance between the two objects) the same amount as we increase the kinetic energy (by increasing the tangential speed), therefore leaving the total energy of the system unchanged. Note, that we could do the inverse as well. So, bottom line: For a given total energy, the orbiting body can ether be close to the central object and have a high tangential velocity, or be far away with a lower tangential velocity (see Keppler's 3rd law if you want to know more about how distance and velocity are related).

So, back to the three body problem. To understand why the small mass is in a stable equilibrium state, you might draw an equilateral triangle or look at the satellite in this picture: Since the centre of mass (around which each of the object orbits) is NOT in the centre of the very big mass, the orbit of the 3rd mass (the moon) is slightly inside the orbit of the small mass (in the picture, the orbit of the moon is slightly inside the orbit of the satellite). If now we move the satellite along its trajectory towards the moon, we do not modify its radial distance and thus not change its tangential velocity (according to what was mentioned above). What we do is we bring him closer to the moon AND further away from the earth. Since the satellite does rotate around the moon (also clockwise, to get an idea of that, imaging yourself on the moon and try to figure out how you would see the satellite.) by bringing him closer, we decrease the potential energy between moon-satellite, which leads (since energy conservation) to an increase in tangential speed (clockwise around the moon), thus the satellite tends to move away from the earth (and the centre of mass). By moving away from the earth we increase its potential energy with respect to the earth, which makes him rotate slower around the earth, thus he tends to move away from the moon (since the rotation he describes around the earth is also clockwise. By moving away from the moon, we increase the potential energy between satellite-moon, thus decrease the angular velocity. The satellite tends to move towards the earth, decreasing the potential energy in the system satellite-earth, thus increase of angular velocity bringing him closer to the moon,... and we are back at the beginning.

So following this line of thought it might get clearer why these points are stable (by the way, it does not depend upon the direction of the rotation, try to think it through with counter-clockwise rotation). Unfortunately this is not the end of the story: You could make the same Gedankenexperiment independent on the actual masses of moon and earth and you would always find a stable point. What actually is important, is the mass ration between the two masses. It is only in a rather small range, where the point is stable. For many systems the change in distance between satellite-moon could not be counterbalanced by the resulting change in tangential velocity (leading to a compensating change in distance between satellite earth) and the satellite would leave the point and ether start to orbit around the moon or the sun. Well, if you want to know exactly how it works, check out the math behind. This is a nice description of the phenomenon.

Hope that helped.

By the way: Note that the Coriolis force does NOT exist. It has to be introduced when one uses an accelerated reference system, to compensate the acceleration of the reference system. Typically, we'd need to introduce this fictional force when choosing the earth or the moon as reference system (they both are accelerated since they rotate around each other.) I'd recommend not to start to include such non-existing forces, since you might risk to confuse them with real ones. Use the centre of mass as a reference system, and describe the system with the use of spherical coordinates. When deriving the unit vector, you'll see 'strange' terms that have to be included for the acceleration. When then using Newton 2nd law, these therms stay on the side of the acceleration and there is no need to invent some new forces.

Answer 7

I think what is confusing you is the rotating reference frame... The L4 and L5 points are rotating around the center of mass (COM) of the Earth-Sun system at the same speed as the Earth and Sun orbit around each other. So when you do the thought experiment of what happens to a point mass at L5 or L4 if infinitesimally displaced, it is easier to think of an inertial reference frame. If in the image above the Earth is rotating counterclockwise, this is a qualitative description of what happens to a point mass moved slightly from L5:

• if displaced slightly away from/closer to the COM, it would not have enough/have too much tangential velocity for its new position, and so would start falling behind/getting ahead of L5, i.e. moving clockwise/counterclockwise.
• if displaced slightly ahead/behind of L5, i.e counterclockwise/clockwise around the COM, its velocity will no longer be tangential to its orbit, so it would start drifting away from/closer to the COM.

Combine this together, and you get that an object displaced from its position at L5 will go into a clockwise orbit around L5. This orbit is stable if the ratio of the masses is larger than ~25.

Answer 8

As I know, in L4,L5 , the potential of the Gravitational power is at it's maximum, although it is unusual for kinematics, that considers stable points to be when U->Min , but in Dynamic systems, stable points can be even when U->Max , but then we call it "Dynamical Equilibrium" in sense that the object will actually move around the stable point (but will never become at the stable point itself, even after passing infinite time) (there is also other differences of the classical stable points). Mathematically, this can be proved by using Lyapunov definition of stability for Dynamical Systems.

P.S I never did that by my self but our professor spoke about this issue during our course of Astrophysics.

Answer 9

I think the fact that you're forgetting (which is easy, I just read the article to find it!) is that in an orbit, angular momentum is conserved. So if an object at $L_4$ or $L_5$ is perturbed inwards, say, then it speeds up slightly and later crosses the orbit. But then it slows down again. In the rotating frame of reference, there's some movement about the Lagrange point but it represents motion about the stable point.

In contrast to the collinear Lagrangian points, the triangular points (L4 and L5) are stable equilibria (cf. attractor), provided that the ratio of $M_1/M_2$ is greater than $24.96$. This is the case for the Sun-Earth system, the Sun-Jupiter system, and, by a smaller margin, the Earth-Moon system. When a body at these points is perturbed, it moves away from the point, but the factor opposite of that which is increased or decreased by the perturbation (either gravity or angular momentum-induced speed) will also increase or decrease, bending the object's path into a stable, kidney-bean-shaped orbit around the point (as seen in the rotating frame of reference).

Answer 10

First some general remarks, then I will discuss the L4/L5 point motion specifically.

I will refer to the three bodies of the three body system as ' the primary', 'the secondary', and 'the tertiary'.

We have that in order for the L4/L5 orbiting motion to persist the mass ratio between the primary and the secondary must be 24.96 or higher.

When the mass ratio is smaller than that 24.96 then eventually the tertiary ends up receiving a gravitational assist that ejects the tertiary from the system.

(Some years ago I created a L4/L5 Lagrange point simulation. The simulation corroborated the predicted behaviour: mass ratio larger than 25: tertiary remains in the system. Mass ratio smaller than 24, tertiary ends up being ejected. I very much enjoyed watching the scenarios play out.)

From here on everything I discuss is for the case of a suffiently large mass ratio, so that the L4/L5 orbiting motion persists.

It is essential to be aware that the motion of the tertiary is never an exactly repeating orbit. The motion of the tertiary has the same type of chaotic character as the general three body problem.

I recommend thinking about L4/L5 orbiting motion in terms of: there is no escape. It's not that the motion is stable: but there is no escape.

Now to the explanation of the L4/L5 Lagrange point motion specifically.

As we know there are two attraction regimes that give rise to closed orbits:

• inverse square law of attraction
• attraction according to Hooke's law

As we know: with an inverse square law the orbiting motion is along an ellipse, with the point of attraction at one focus.

The fact that with an inverse square law of attraction the orbiting motion is an exactly repeating orbit is an essential feature.

To illustrate that I discuss a thought demonstration.
Let a spacecraft be in orbit around a celestial body, let's make that the Earth. Let the initial orbit be a circular orbit, Low Earth Orbit, it takes the spacecraft about 90 minutes to complete a cycle.

Next the spacecraft fires its rocket engines for a number of seconds, increasing the velocity of the spacecraft.

The effect of that is that the circular orbit gets changed into an ellipse-shaped orbit, with its perigee at the point where the burn was executed. The resulting motion is cycling with perigee always at the same spot.

What I mean with 'the same spot' is that the orientation of the ellipse shaped orbit with respect to the fixed stars remains the same. (Of course in the actual solar system there are all kinds of perturbations; for the purpose of the thought demonstration those are ignored.)

The point is: there is a strong element of inescapable to orbiting motion.

If you are in a spacecraft, and you do a small burn, then the nature of the orbiting motion is that after a full cycle the orbiting motion brings you back to the point in the previous orbit where you started from.

That the-cycle-brings-you-back property is a general property of orbiting motion.

I cannot emphasize this enough:
When you are in orbit and there is a transient push on you then after a full orbit cycle the orbital dynamics brings you back to the point that you were pushed away from.

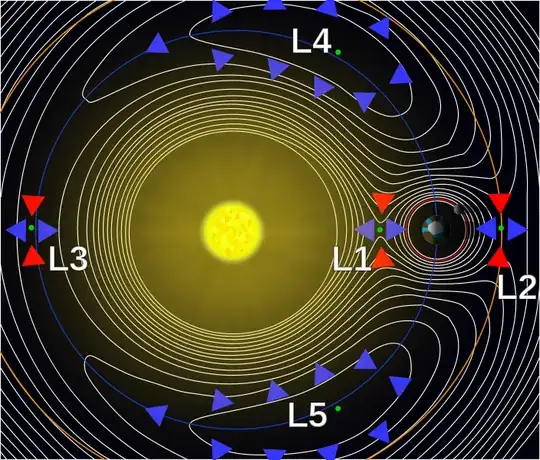
Imagine a tertiary that is initially orbiting very close to the L4 (L4 is 60 degrees ahead of the secondary)

The combination of the gravitational attractions from the primary and the secondary is such that it is energetically favorable for the tertiary to either start lagging L4, or to start pulling ahead of L4.

Once the tertiary starts lagging behind L4 the distance to the primary increases, and the distance to the secondary decreases. That means that once the tertiary start lagging behind L4 the lag tends to increase.

It isn't possible for the tertiary to remain in exact co-moving motion with the L4 point. For the tertiary to orbit exactly at the L4 point is similar to the case of a marble sitting on top of a dome. It is inevitable that the marble starts rolling down the dome. Likewise, for a tertiary that initially is co-moving with L4: inevitably the tertiary will start lagging behind the L4 point, or start pulling ahead of the L4 point.

But: we are dealing with orbiting motion here.
The tertiary is initially orbiting at the L4 point, and it gets pushed away from the L4 point, and then the orbital mechanics brings the tertiary back to where it came from.

(The description above was for the L4 point, the reasoning generalizes to the L5 point)

The same occurs when the tertiary is pushed away from the L4/L5 point in radial direction. Each time such a push happens the dynamics of orbiting motion brings the tertiary back to where it came from.

That is what I mean when I describe the L4/L5 orbital motion as 'it's not stable, but there is no escape'.

When the mass ratio between primary and secondary is sufficiently large the push away from the L4/L5 point is weak, and the orbital dynamics effect can undo it; the tertiary is returned to the L4/L5 point.

When the mass ratio between the primary and the secondary is small then the push away from the L4/L5 point is more than the orbital dynamics effect can counter.

With small primary/secondary mass ratio: when a simulation is started (starting with the tertiary at the L4/L5 point): once the tertiary rolls of the L4/L5 point it starts straying further and further away from it. The end result is ejection from the system.

Simpler case: circumnavigating motion with Hooke's law

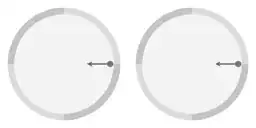
Picture 1. Animation

In the animation:
The disk with 4 quadrants along the rim represents a platform, any platform. The dark dot represents an object that is circumnavigating a point of attraction. The arrow represents the magnitude and direction of the force that is being exerted.

The left hand side of the animation shows the actual motion of the object. The right hand side of the animtion shows the motion of the object relative to a coordinate system that is rotating with the same period as the circumnavigating motion of the object.

While the circumnavigating object doesn't have a constant angular velocity it does have a regular orbital cycle; the angular velocity of the rotating coordinate system (right hand side) matches the duration of that cycle.

We have in the case of one-dimensional motion: Hooke's law gives harmonic oscillation.

The motion displayed on the left hand side of the animation is two-dimensional motion, and it can be described as a superposition of two harmonic oscillations, at right angles to each other:

$$ x = a \cos(\Omega t) \quad \text{and} \quad y = b \sin(\Omega t),$$ where

$a$ is half the length of the major axis
$b$ is half the length of the minor axis
$\Omega$ is $360^\circ$ divided by the duration of one revolution.

The following diagram illustrates the major axis and the minor axis:

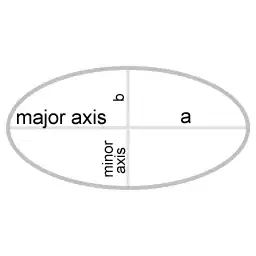
Picture 2. Diagram

The description above can be rearranged as follows:

$$ x = \left( \tfrac{a+b}{2} \right) \cos(\Omega t) + \left( \tfrac{a-b}{2} \right) \cos(\Omega t) $$ $$ y = \left( \tfrac{a+b}{2} \right) \sin(\Omega t) - \left( \tfrac{a-b}{2} \right) \sin(\Omega t) $$

The following animation illustrates the rearrangement:

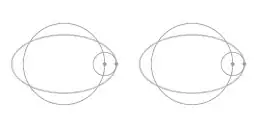
Picture 3. Animation

Repeating the animation with the quadrants:

The motion with respect to the rotating coordinate system (right hand side):

$$\begin{align} x &= \left( \tfrac{a-b}{2} \right) \cos(2 \Omega t) \\ y &= - \left( \tfrac{a-b}{2} \right) \sin(2 \Omega t) \end{align}$$

Notice especially that when the central attracting force is according to Hooke's law the motion relative to the rotating coordinate system (right hand side) cycles twice for every cycle of the circumnavigating motion (left hand side)

The next step is to obtain an expression for the acceleration of the moving object relative to the co-rotating coordinate system.

Let $a_c$ be the acceleration relative to the co-rotating coordinate system.

We take advantage of the fact that the motion along the epi-circle is, in the idealized case, perfectly circular motion.
In the case of circular motion, the acceleration is perpendicular to the velocity and has this magnitude:

$$ a_c = \omega^2r \tag{1} \label{eq:1}$$

(I use the lowercase $\omega$ here for the motion along the epi-circle to distinguish it from the uppercase $\Omega$ that I used for the angular velocity of the system.)

As stated earlier, the motion along the epi-circle occurs at twice the frequency of the angular velocity of the system: $\omega = 2\Omega$.

Inserting that into \eqref{eq:1}:

$$ a_c = (2\Omega)^2r \tag{2}\label{eq:2} $$

Let $v_c$ be the velocity of the object relative to the co-rotating coordinate system. We have the general relation $v=\omega r$. We have, in this case, $\omega=2\Omega$. Combining that gives for this case the expression $ 2\Omega r = v_c$, that we can use to modify \eqref{eq:2}.

After substituting, we obtain the following expression for the acceleration of the object with respect to the co-rotating coordinate system:

$$ a_c = 2\Omega v_c \tag{3}\label{eq:3} $$

I'm bringing all of this up because there is a common theme: closed orbit.

Both with an inverse square law (of attraction) and with Hooke's law the resulting motion is a closed loop.

In the case of Hooke's law (3) gives the acceleration with respect to the rotating coordinate system. That is: for the motion with respect to the rotating coordinate system (3) gives the acceleration factor that is associated with the object being returned to where it came from.

(3) describes that in the case of circumnavigating motion subject to a central force there is a relation between velocity with respect to the rotating coordinate system and acceleration with respect to the rotating coordinate system.

---

[Later edit]

The image below is for the case of a primary and a secondary, with the secondary orbiting with a slightly eccentric orbit. The motion shown is the motion with respect to the rotating coordinate system that is rotating with the same period as the secondary.

The image is a screenshot from the orbital motion simulation that I mentioned earlier in this answer.

The motion with respect to the rotating coordinate system is not along a circle; the shape is elongated.

(It is only in the case of a central force according to Hooke's law that the motion wrt the rotating coordinate system is along a (small) circle.)

The image below is again a screenshot of the simulation. It displayes motion of the tertiary with respect to the Lagrange point.

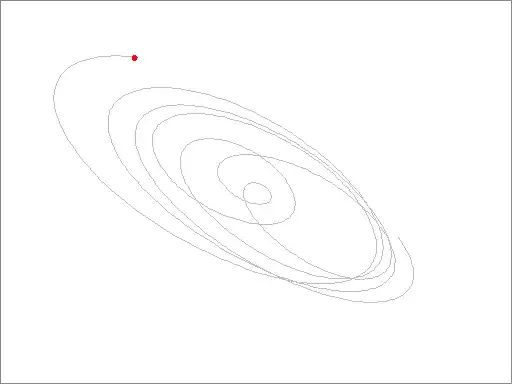
We have that the motion of an actual tertiary around the Lagrange point has a chaotic property; the motion is constrained to a region, but within that region long term prediction is not possible. The path that the simulation yields has that chaotic property.

Why L4/L5 motion persists

The thing that is unique to the L4/L5 points is that there is a symmetry: the gravitational influences from the primary and the secondary combine in such a way that the tertiary is pulled away from the L4/L5 point in either direction. Combined with that: the orbital dynamics always brings the tertiary back to the L4/L5 point. No escape.

For any other point in the primary/secondary system, including the L1, L2, and L3 points, that symmetry is not there. That allows drift to accumulate.

The accumulation issue is the key:
For any point in the primary/secondary system: drift of a tertiary can accumulate. The L4/L5 regions are the only regions where symmetry of the force effects prevents drift from accumulating.