In the Quantum Electrodynamics theory, the repulsion between electrons is caused by the exchange of photons. This exchange can be represented with the help of Feynman Diagrams, but why the electron has to necessarily emit a photon towards other electron when two of them approach each other?
2 Answers
Let us start with two free electrons approaching each other.
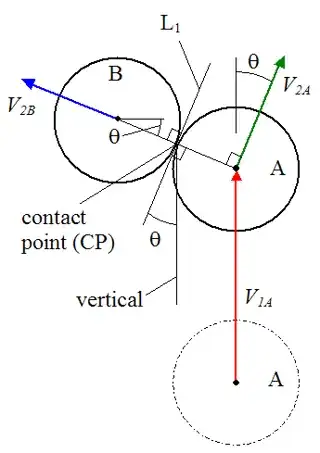
If they were classical billiard balls we could draw a graphic of the incoming and outgoing directions of the billiard balls.
B ball is at rest and is hit by A.
If you read the link on the analysis, the point of impact, the radius etc determine the result .
We thus can predict with classical mechanics , given the contact point and the angle of incidence, how the two balls will scatter of.
The electrons are elementary particles , quantum mechanical entities. There are few measurements we can do on such small entities, and one of them is to measure the scattering amplitude, i.e. what is the probability when an e- "hits" an e- that they scatter off at an angle theta. Probability, not prediction for a single event, but for an accumulation of events. This started to be described mathematically by the scattering matrix back in 1939.
It is immediately connected with an interaction picture, where given a hamiltonian the solutions will show probability distribution of the particles under consideration . If you look into the mathematics and the expansion series this is a laborious process when trying to calculate specific cross sections of nuclear reactions , and specifically for the Manhattan project where Feynman with a lot of top physicists were "conscripted" . Notice there are only inputs and outputs for the scattering matrix, just like the billiard balls.
Feynman had an "aha" moment ( see below) and saw that a representation of the terms of the expansion of the S matrix , starting with the lowest order giving the highest contribution to the probability, would simplify the calculations, if iconic exchanges of the quantum numbers and energy momentum were represented as internal lines , i.e instead of having in the center of mass X, two incoming and two outgoing , one could expand the dot in the middle, which carries the quantum numbers, into the first order exchange, and add as necessary the higher orders as loops exchanging quantum numbers. This cleared the confusion because the accompanying vertex functions had the couplings and the strength in the contribution of each term became clear.
In the case of e- e- scattering the quantum numbers of the dot in X are the ones of a photon and it was dubbed a "virtual photon" exchange for the first order diagram, to make sure there was no confusion with particles . The virtuals in higher order diagrams can be many different lines carrying the quantum numbers of their name, except being off mass shell and under integrations in the limits of the integral. So it is a mathematical construct that brought order into a large number of integrals to be calculated if one wants a specific crossection. There are no emissions, just propagators under integration that are identified with the named particle and will generate a resonance when the energies of scattering are close to the mass of the named particle.
Now repulsion and attraction depend on the potential, as is the case in classical electromagnetism, and the wavefunctions of the attractive potential
solution will be different than the ones for the repulsive.
The aha moment of Feynman:
I have been fortunate to be at a workshop where Feynman was participating,back in the early '80's and he was full of stories, at the informal times of coffee etc. This story is as I remember it:
When he was in the Manhattan project , the calculational jobs for the S matrix were apportioned to several physicists, an early form of parallel computing. Once a week they would get together and present their calculations for the required proccess, compare the results and put them in the report. They needed a week to get through the integrals. Then he had the aha moment. He described it so vividly that I have a picture of him in my memory . He said that he "used to lie on his bed with feet on the wall," and suddenly he saw the complete picture of what we know now as feynman diagrams for the expansion. He immediately took the problem he had been handed and solved it in a day. He told the results to the other who had been given the same problem, and they were amazed that his result was correct even though he had only worked on it for a day and they had worked for a week.
He laughed, and said "I did this a few times before showing them my method!" He was a great teenager even when I met him.
- 236,935
Each charge is a source of a force field acting on the other charges, immediately or with retardation, whatever. It is an experimental fact.
The total field of a charge can be represented as a near field (virtual photons) and the radiated field (real photons).
The real photons are never absorbed, but scattered. The virtual photons are always absorbed, roughly speaking.
- 14,125