After reading this question, I realized that I didn't really understand how a MOT works in detail. I was always relying on the simplistic picture given in textbooks which never addresses the actual polarization of the light: they seem to make no difference between $\sigma^{+}$/ $\sigma^{-}$ (which normally refers to atomic transitions) and the polarization of light.
Knowing that the circular polarization of the beams that is along the axis of the anti-Helmholtz coils (I will refer to that pair of counter-propagating beams as the "on-axis beams" from now on) needs to be the opposite of the circular polarization of the off-axis beams (if the on-axis beams are clockwise, the off-axis beams should be counterclockwise), I tried to figure out how a MOT was really working. However, my explanation seems to be in contradiction with the usual explanation presented in textbooks, so I would like to know if I'm getting something wrong.
Here is my understanding of the MOT:
First of all, a pair of anti-Helmoltz coils generates a quadripolar field that looks like that (that drawing was taken from Bill Phillips Nobel lecture):
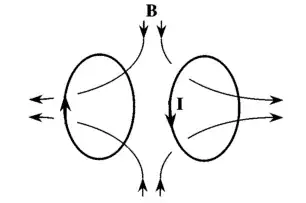
What is important here is that the on-axis B-field is pointing outwards and the off-axis B-field (in the median plane between the coils) is pointing inwards (this can be reversed by changing the direction of the current).
For the rest of the discussion, let's assume that this is how the B-field is (pointing outwards on-axis, inwards off-axis).
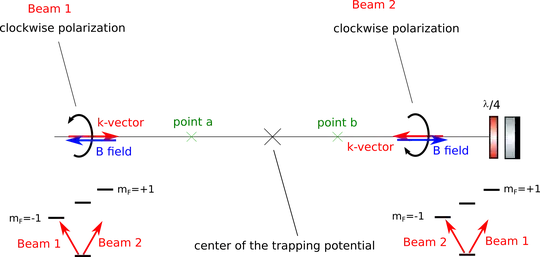
We now need to know what transitions the different lasers will drive. This depends on the polarization of the light, but also on the respective orientation of the k-vector and the B-field (all the polarizations are defined from the point of view of the observer. This is the convention I will take for the rest of the discussion):
I am still unsure about this drawing so please let me know if I'm wrong.
Now let's see how the trapping works.
First, here is what happens on-axis :
Both counter-propagating beams have the same polarization (as you get a $\pi$ phase shift upon reflexion on the mirror plus another $\pi$ phase shift by going through the quarter-wave plate twice).
point a:
The k-vector of beam 1 and the local B-field are pointing in opposite directions, and beam 1 has a clockwise polarization. This means that beam 1 is driving a $\sigma^{-}$ transition.
The k-vector of beam 2 and the local B-field are pointing in the same directions, and beam 2 has a clockwise polarization. This means that beam 2 is driving a $\sigma^{+}$ transition.
Thanks to the Zeeman shift, this means that beam 1 is closer to resonance with $m_{F}=-1$ than beam 2 is with $m_{F}=+1$. As a consequence, the atoms absorb more photons from beam 1 than from beam 2 and thus tend to move towards the center of the trap.
point b:
The k-vector of beam 2 and the local B-field are pointing in opposite directions, and beam 2 has a clockwise polarization. This means that beam 2 is driving a $\sigma^{-}$ transition.
The k-vector of beam 1 and the local B-field are pointing in the same directions, and beam 1 has a clockwise polarization. This means that beam 1 is driving a $\sigma^{+}$ transition.
Again, the atoms are brought towards the center of the trap.
Now let's see what happens off-axis :
point a:
The k-vector of beam 1 and the local B-field are pointing in the same directions, and beam 1 has a counterclockwise polarization. This means that beam 1 is driving a $\sigma^{-}$ transition.
The k-vector of beam 2 and the local B-field are pointing in opposite directions, and beam 2 has a counterclockwise polarization. This means that beam 2 is driving a $\sigma^{+}$ transition.
point b:
The k-vector of beam 2 and the local B-field are pointing in the same directions, and beam 2 has a counterclockwise polarization. This means that beam 2 is driving a $\sigma^{-}$ transition.
The k-vector of beam 1 and the local B-field are pointing in opposite directions, and beam 1 has a counterclockwise polarization. This means that beam 1 is driving a $\sigma^{+}$ transition.
The problem I have is that this explanation is the only self-consistent explanation I could find that also matches what experimenters do (that is: having the polarization from the on-axis beams the opposite of that of the off-axis beams), but it goes against textbooks (or at least, they don't explain their reasoning enough for me to be able to understand the details). For instance, most of them say that, on one side of the center of the trapping potential, $E_{m_{F}=+1}>E_{m_{F}=-1}$, while on the other side $E_{m_{F}=-1}>E_{m_{F}=+1}$, which contradicts my model. I suspect that most differences between my model and the simplistic one presented in textbooks arise from the fact that they take a global quantization axis, while I use the local B-field as a local quantization axis, but I'm not familiar enough with this kind of problems to be sure.
Is there something wrong with the explanation presented above?
If needed I can take some examples from textbooks and pinpoint exactly why they disturb me, but I think this question is already long enough.