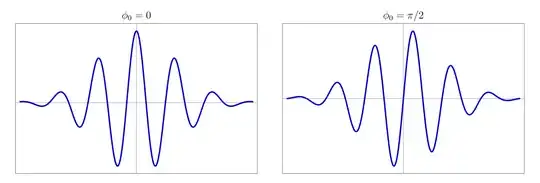
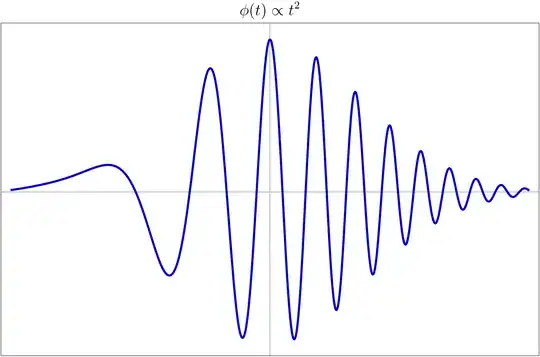
An ultrashort laser pulse can usually be written as a product of a time-varying envelope $A(t)$ and a periodic function with angular frequency $\omega$
$$E(t)=A(t)\cos(\omega t+\phi(t)+\phi_0)$$
Where $\phi(t)$ is temporal phase and $\phi_0$ the absolute phase .
(I found this kind of expressions in the book Ultrafast Nonlinear Optics, by Reid, and in the PhD thesis Ultrashort pulse characterization in amplitude and phase from the IR to the XUV.)(25th page)
My question is why this is so? What is the basis? I cannot understand the importance of $\phi(t)$ and $\phi_0$.
Pictorial approach is welcomed.