The only time we need to know where a force acts is when we are calculating a torque. For contact forces, it is clear that the force acts at the point of contact. But for a force like gravity, that acts at a distance, it is less clear.
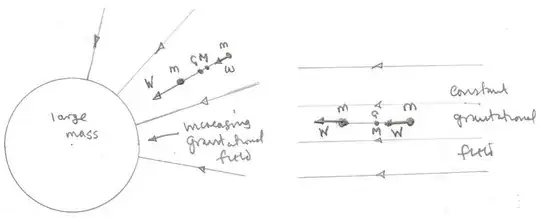
In reality, a rigid object is made up of many particles, and there is a small gravitational force and torque on each of them. When we only care about acceleration we only need the sum of all these forces, which is $\vec{F}_{tot} = \sum_i m_i \vec{g}= M\vec{g}$. But what about the torques?
We would like to pretend that this total gravitational force acts at a single point for the purpose of calculating torque. Is there a point $\vec{x}_{cg}$ such that $\vec{x}_{cg}\times \vec{F}_{tot}$ gives the same total torque as summing up all the small torques?
If we do sum up all the torques we find $\vec{\tau}_{tot} = \sum_i \vec{x}_i\times (m_i\vec{g}) = \left(\frac{1}{M}\sum_i m_i \vec{x}_i\right) \times (M\vec{g})$. This tells us to call $\vec{x}_{cg} = \frac{1}{M}\sum_i m_i \vec{x}_i$ the center of gravity, and if we pretend that the total force of gravity acts at this point, it will always give us the right answer for the gravitational torque. Finally, we notice that it happens to have the same form as the definition of the center of mass!
However! If you do the calculation yourself you might notice that if $\vec{g}$ varies from particle to particle then this derivation does not work. In this case the center of gravity is not actually well defined. There may be no $\vec{x}_{cg}$ that does what we want, and even if there is it is not unique, except in a few special cases.