Why is Hubble's Constant exactly the inverse of the age of the universe?
This cannot be coincidence. If according to our laws of physics this is coincidence then surely we have got something worked out wrong.
If this 'coincidence' were to continue, it proves that Hubble's Constant must be decreasing. Furthermore, does it imply that expansion if the universe is asymptotic?
Hubble's constant is probably a little larger than the inverse of the age of the Universe. The reason they are close is somewhat of a coincidence, for example in the standard Lambda-CDM model of the Universe, in the far future the age of the Universe will become vastly larger than the inverse of the Hubble constant, because H asymptotically approaches a constant value.
The dynamics of the standard dark energy models, in which over time the accelerated expansion caused by dark energy dominates, but the expansion in the early Universe was decelerating due to the domination of radiation and then matter, means that at some point the inverse of the Hubble constant must equal the age of the Universe. It just so happens that in cosmological terms that point is very close to the present time and so the two are close to equal.
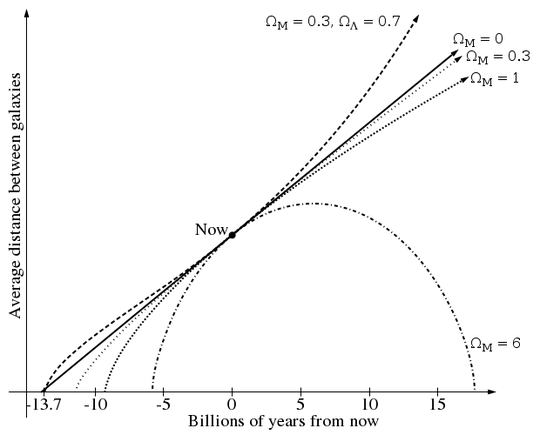
In the below graph from Wikipedia, you can see that the start of the curves representing $\Omega_M = 0$ (the Milne model, where the age of the Universe is the inverse of the Hubble constant) and $\Omega_M = 0.3, \Omega_{\Lambda} = 0.7$ (a standard cosmological constant model of dark energy) very nearly coincide.
Hubble's law is the rate of expansion of the universe. If you assume it expanded from a point then the inverse is the time since it was zero size.
It's a little more complicated because the rate isn't constant with time , see Estimating age of the universe by Hubble's law?
For a 4-D sphere (or bubble) expanding radially at the speed of light:
r (radius) = 4230.53 Mpc (13.8 billion light years)
Given that c.2PI would also be the expansion around the "skin" (our 3D universe) then Hubble's constant can be calculated as rate of change over total change:
c.2PI / r.2PI = c/r = 70.864 (km/sec)/Mpc (Hubble's constant)
If you look more closely at c/r the units are inverse time.
In fact it simplifies to 1 / age of the universe.
