Why do insulators have "just enough" electrons to fill the valence band

Question

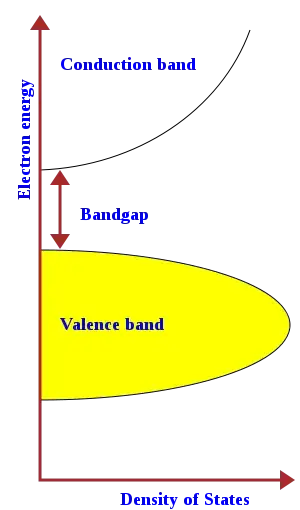
This is the classic picture of the band structure for an insulator (or semi-conductor):

The common explanation as to why this doesn't conduct is that the electrons fill the valence band perfectly full so that it is a traffic jam, and that there is not energy to excite electrons from the valence to the (empty) conduction band. The fermi energy level is somewhere in the bandgap.

However, why would we have just the right amount of electrons to fill the valence band but no more? This seems like too much of a coincidence given that insulating crystals are very common materials.

Supposed we doped the material to increase the charge carriers slightly. It appears that some electrons would be forced into the conduction band. But a small amount of doping doesn't make i.e. diamond a conductor (not even a poor conductor).

Perhaps the band structure "adjusts itself" (through electron interactions, etc) to perfectly fill the valence band? Or am I interpreting the diagrams incorrectly?

Answer 1

A simple answer to your question is that each band can contain $2N$ electrons of the system, while the number of electrons that are available to fill up the band is $ZN$, where $Z$ is the valency of the atom.

I will try to be a little more specific now. What I was assuming was the 'tight-binding model', which, in the 1-dimensional case (easily generalised to the 3-dimensional case), consists of $N$ sites in a line (or lattice in higher dimensions), separated by a lattice spacing $a$. The electrons can be attached to one of these sites, and may 'hop' from its current lattice site to the neighbouring ones. The Hamiltonian takes the form

$$H = E_0 \sum_n |n\rangle\langle n| -t\sum_n(|n\rangle\langle n+1| + |n+1\rangle\langle n|).$$

where $E_0$ is a constant, $t$ is called the 'hopping parameter'.

For $N$ atoms, this system has $N$ (ground) states. However, an electron can be in spin up or spin down. Now, the Pauli Exclusion Principle does not permit any two electrons to occupy the same state, so the $N$ (degenerate) ground states (or 'band') accommodate $2N$ electrons.

If a material has valency $Z = 1$, then each of the N atoms release a free electron. The ground states are therefore half filled, and we have a half-filled band. If $Z = 2$, then there are $2N$ electrons and we have a filled band, which is exactly what is depicted in the diagram in the question.

Of course, there are higher energy states and $Z$ can be greater than $2$. In general, fully filled band(s) are called the valance band(s), while a partially filled band is called a conduction band.