2

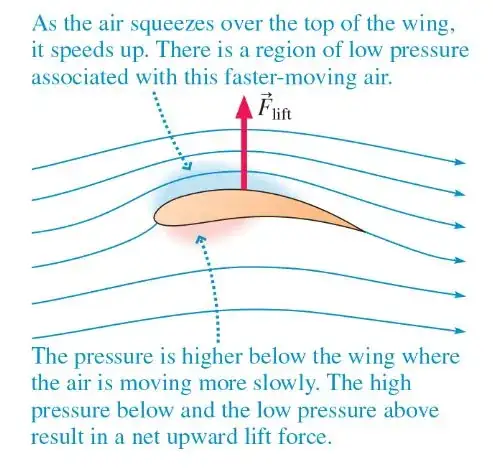
In my physics textbook, there's a chapter on fluids which discusses pressure, flow rate, continuity, and the Bernoulli effect. I understand why pressure gradients induce net force on a column of fluid and why that subsequently causes the speed of the fluid to increase as it enters the low-pressure area.

The book goes on to mention some implications of the Bernoulli effect using the example of lift:

enter image description here

Could someone please explain why the speed of the wind increases when it passes over a concave-down shaped structure such as the top of the wing shown here? What exactly causes that speed to increase? I assume it has something to do with the streamlines approaching each other, but why would that cause acceleration?

Aleksandr Hovhannisyan
  • 316

2 Answers2

1

In the case of concave down part

The fluid that was initially flowing would have to shift a little bit upwards where there already exists fluid that was any way moving in that direction so at close approach to the surface there is same amount of fluid moving through lesser space and then we know

A1V1 = A2V2

Hence velocity increases similar way you can think for lower surface

Hope you can visualise

Utkarsh futous
  • 415
1

There is a very nice interpretation of this in 2D potential flow theory. The streamlines correspond to specific values of Lagrange's stream function $\psi$. it is defined by:

$u = \dfrac{\partial \psi}{\partial y}$ and $v =-\dfrac{\partial \psi}{\partial x}$.

If you calculate the flow rate $Q$ per unit depth from one streamline (A) to another streamline (B)

$Q = \int_A^B[u,v]\cdot[n_x,n_y]ds,$

in which $[u,v]$ is the velocity vector and $[n_x,n_y]$ is the normal vector of the line integral from $A$ to $B$. The normal vector is given by $[dy,-dx]/ds$. Hence,

$Q = \int_A^B[u,v]\cdot[dy,-dx]=\int_A^B udy-vdx.$

Now, apply the definition of the stream function.

$Q = \int_A^B \dfrac{\partial \psi}{\partial y}dy-\left(-\dfrac{\partial \psi}{\partial x} \right)dx$

Observe that the expression in the integral equals the total derivative of $\psi$. So, we obtain:

$Q = \int_A^B d\psi=\psi(B)-\psi(A).$

EDIT: The tighter the streamlines get (we assume the Q is constant from one to the next streamline), due to the concave surface, the smaller will the distance d become. In order to still have constant $Q$ the velocity has to increase.

MrYouMath
  • 352