The title basically sums up the question. We know that if I shoot $N$ particles through a double slit then as $N$ gets large I see an interference pattern. Now if I take $N$ experiments and shoot one particle for each experiment and superimpose the outcome do I still see an interference pattern, or does the set up need to "warm-up" over some early particles?
Asked
Active
Viewed 356 times
3 Answers
2
The interference pattern emerges due to interference of the two wave fronts that emerge from two slits. Even if you shoot one particle at a time in a single setup, the interference pattern will emerge over time, since the single wave-particle interference with itself when passing through the slits.
Thus, if you have N experiments, where in each setup a single particle is shot, the aggregated interference pattern will be equivalent to the case where a single particle is shot at a time. So you will see the interference pattern.
user3394040
- 732
1
Theoretically, yes, the interference pattern should emerge if you shoot one particle in each of $N$ experiments and then merge the outcomes.
However, It is not practically feasible to conduct thousands, or millions of experiments using one particle each. So, this can not be experimentally verified.
But, what can be done for reasonable experimental proof is - conduct (say)100 experiments (with identical setups) with few hundred/thousand/million particles in each and then superimpose the outcomes.
QM community is convinced to an extent that is beyond any level of scrutiny, and it would not see any point in conducting such an experiment. So, this is not likely to happen.
kpv
- 4,529
-1
What exactly is meant by "seeing" an interference pattern?
Experimentally, it means this: You throw the particles at the two slit apparatus. You then set up a continuous array of detectors on the screen. The detectors give you a binary answer. They tell you if they collected the particle or not. Thats it. They certainly don't show you any pattern!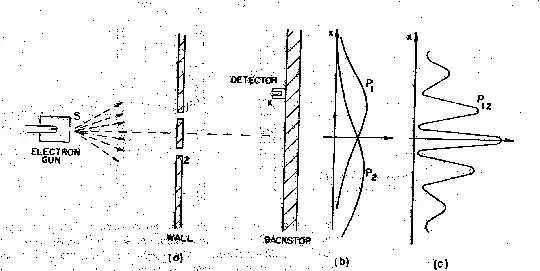 
You then plot the number of particles you collected against position after throwing many many particles. The plot you get when slit 2 is closed is plotted as $P_1$ and when slit 1 is closed is plotted as $P_2$ in figure(b).
If both were kept open the result is plotted in (c). This has a striking resemblance to our familiar interference pattern(And with good reason, it is the probability amplitudes that are interfering). This is often why it is referred to as interference.
The big lesson here is that this interference is inherently a statistical phenomenon. You simply can't obtain this pattern with one particle. It doesn't matter if you did the experiment with one set up or a different set up every time. Nature is inherently probabilistic, assigning in some manner the probabilities of going to a certain point. These are probabilities that you can "see" when you do sufficient re trials of the experiment with sufficient number of particles, using any number of identical apparatus in any order you like. The answer is the same. It certainly has nothing to do with memory, since we assume that in each particle reaches our detector independently of others.
Anonjohn
- 764