Why does torque point perpendicular to direction of the motion?

Question

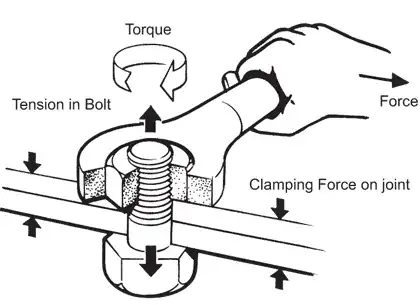
I have an intuition problem calculating torque using the cross product formula. As for example let the magnitude of the force be 50 lbs and length of the wrench be one foot and you are exerting force in a clockwise motion and the angle you apply the force 60 degrees. This is an example so I can ask my question. Using the right hand rule the torque points perpendicular to the force you are applying to the bolt. In this case since the sine of 60 degrees is about .86 it would be (.86)(50) foot lbs. How can the bolt turn clockwise if the force is concentrated perpendicular to where it needs to turn? The cross product formula demands the torque be perpendicular. Obviously my mistake but I don't see where.

Answer 1

To add to Steeven's answer and in particular his very pertinent statement:

You can't define a vector direction as something that turns around.

It may help you to understand that torque as a vector is actually cheating a little bit: it's a "simplification" that we can only get away with in two and three dimensions, which is why the "direction" seems a little abstract. The torque "vector" direction defines the axis of the motion that it tends to induce, and for the same reason that torque as a vector is a bit of a trick, even the notion of axis only works in two and three dimensions.

Torque is about rotation, and rotations primarily are about transformations that are confined to planes. For example, a rotation about the $z$-axis is a transformation that churns up the $x-y$ plane - it transforms the $x$ and $y$ co-ordinates of things - but leaves the $z$ co-ordinates unchanged.

When we do higher dimensional geometry, rotations change planes and leave more than one dimension invariant. In a four dimensional rotation, it's incomplete to speak of a rotation about an axis, because, for example, you can have a rotation that transforms the $x$ and $y$ co-ordinates of points invariant, but it leaves the $z$ and $w$ co-ordinate invariant.

So, in general, the easiest way to specify a rotation is by specifying the plane that it changes, rather than specifying the subspace that it leaves invariant.

It just so happens that in three dimensions, the subspace left invariant is a line or an "axis"- so the two approaches amount to the same thing. We can define a plane in three dimensions by specifying a vector normal to it, which is why we can get away with a torque or angular velocity as a vector. In general these quantities are directed planes, not lines with direction.

Answer 2

How can the bolt turn clockwise if the force is concentrated perpendicular to where it needs to turn?

Because that force is perpendicular to the direction towards the rotation-centre. Not to the turning direction. The bolt does indeed turn in the same way as the force pulls it.

When you define a torque vector direction, you have a problem. You can't define a vector direction as something that turns around. The direction must be along a straight line. So instead of choosing the torque "turn", we could choose the torque axis as the vector direction.

Have a look at this picture:

The axis is vertical through the bolt along the two upwards/downwards arrows. If you choose to define the torque vector direction along this axis, all fits. We just have to remember that choice.

Torque is: $$\vec \tau = \vec F \times \vec r$$

The force vector $\vec F$ times the vector towards the rotation-centre $\vec r$ gives the torque vector. The result of a cross-product is mathematically a vector pointing vertically upwards, so this fits perfectly to that choice. The torque vector $\vec \tau$ that you get from this calculation has the torque magnitude but the torque-axis direction.

As long as you remember this choice - this definition - all is good. Everytime you hear "the direction of the torque is horizontal", you know that this is only the axis of the torque; the torque (the turn) is then upright.

Answer 3

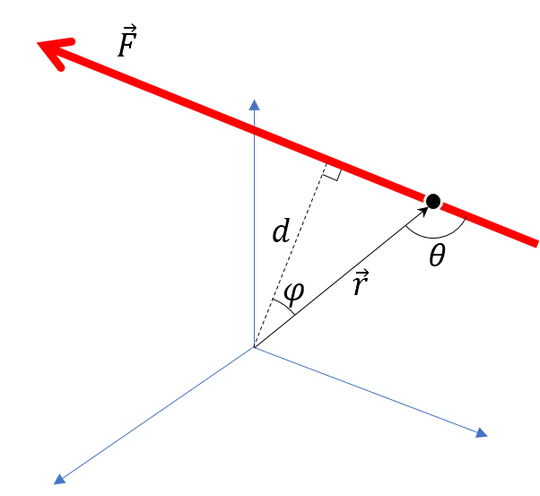
Consider the definition of torque $\vec{\tau}$ due to a force $\vec{F}$ passing through a point $\vec{r}$ $$\vec{\tau} = \vec{r} \times \vec{F}$$

Using the cross product identity $\| \vec{A} \times \vec{B} \| = \| A \| \|B \| \sin \theta$ where $\theta$ is angle formed by the two vectors we can write the following

$$ \| \vec{\tau} \| = \| \vec{r} \| \| \vec{F} \| \sin \theta $$ $$ \tau = F (r \cos \varphi) = F \, d$$ since $\theta = \frac{\pi}{2}+\varphi$ and $d = r \cos\varphi$ is the perpendicular distance to the force line of action.

In Summary, the cross product removes any influcence of the location of the force along the line of action and only considers the perpendicular distance for measuring torque.

Appendix

Torque is the moment of the line of action of a force. It is defined as $\vec{\tau} = \vec{r} \times \vec{F}$

Velocity is the moment of the line of rotation of a rigid body. It is defined as $\vec{v} = \vec{r} \times \vec{\omega}$

Both quantities ($\vec{\tau}$ and $\vec{v}$) contain the information about the distance (position) to a line in space. This can be recovered by

$$ \begin{align} \vec{r}_{\perp} &= \frac{\vec{\omega} \times \vec{v}}{\| \vec{\omega} \|^2} & \vec{r}_{\perp} &= \frac{\vec{F} \times \vec{\tau}}{\| \vec{F} \|^2} \end{align} $$

The direction of the torque vector is similar to the direction of the velocity vector on a rotating rigid body. It is a circumferential vector perpendicular to both the line of action and the location of the line. It is best explained motion motion as the tangential velocity of an extended rotating body under the coordinate origin.

_{See this answer for a more detailed explanation of the geometry in mechanics.}

Answer 4

I believe that your question is best answered by the gyroscope experiments. First, the gyroscope not spinning, is supported on both ends. One support is then removed, and the gyro "falls." However, when this experiment is repeated with the gyro spinning, the gyro, instead of falling, it spins around the supporting end! This motion is perpendicular to both, the gravity force vector and the torque vector. This proves that torque generates a vector that is perpendicular to the plane of rotation.

Answer 5

Why does torque point perpendicular to direction of the motion?

Physicists often say they use first principles thinking, but in order to come up with those first principles, they always use real world observations and create equation(s) to explain the observation, but sometimes cannot explain the fundamental reason behind the observation which gave rise to the equation. In three dimensional space, there are two possible orthogonal vectors (torque vector in this example) relative to another plane (rotating object in this example). The torque vector could potentially be in either direction, thus it's counterintutitive. Our universe (from what humans observe from Earth and outer space in our solar system) just so happens to use the right hand grip rule for the direction of the torque vector. Why? It just is. It might be coincidental that we have other phenomena using this right hand grip rule in the "Interesting Facts" below. It's how the universe was designed. Physicists came up with the equation of T = r * sin(theta) * F by looking at spin procession of a rotating object. It was simply using an analogy they observe on Earth with spinning objects. The first video below explains it very well. The T is simply what they measure torque for the spin procession of each effect. Physicists have not proven why the torque vector points in the direction of the thumb when using the right hand grip rule. It just is. They simply show a value with units based on the math. See second video on how the right hand grip rule works. Video #3 shows a lot more of the mathematics.

Video #1:
https://www.youtube.com/watch?v=ty9QSiVC2g0

Video #2:
https://www.youtube.com/watch?v=fuTVnSFBhwk

Video #3
https://www.youtube.com/watch?v=XPUuF_dECVI

In this case since the sine of 60 degrees is about .86 it would be (.86)(50) foot lbs. How can the bolt turn clockwise if the force is concentrated perpendicular to where it needs to turn?

This is just using the mathematics from the equation T = F * r * sin(theta) in the explanation above. Just make sure to use the correct units (Newton meters) for the torque for physics when solving an equation. Take a look here for conversion units if using foot pounds. https://en.wikipedia.org/wiki/Pound-foot_(torque). If the force vector and the torque vector apply to the same direction as the right hand grip rule, you get a positive torque vector, because there really is a perpendicular force (torque). If it's the opposite direction, you get a negative torque vector. But in reality, the forces are in both directions in physics, since you always have equilibrium with Newton's Third Law. But in mathematics, you need to show which one is positive and which one is negative for the first principles to work out.

---

Interesting Facts with Right Hand Grip Rule:

• (Ampère's Circuital Law) An electric current passes through a solenoid, resulting in a magnetic field. When you wrap your right hand around the solenoid with your fingers in the direction of the conventional current, your thumb points in the direction of the magnetic north pole.
• (Ampère's Circuital Law) An electric current passes through a straight wire. The thumb points in the direction of the conventional current (from positive to negative), and the fingers point in the direction of the magnetic lines of flux.
• (Torque) The principle is used to determine the direction of the torque vector. If you grip the imaginary axis of rotation of the rotational force so that your fingers point in the direction of the force, then the extended thumb points in the direction of the torque vector. This is often referred to as spin precession.
• (Electromagnetic Field) When applying the rule to current in a straight wire for example, the direction of the magnetic field (counterclockwise instead of clockwise when viewed from the tip of the thumb) is a result of this convention and not an underlying physical phenomenon.