Why is distance taken to be perpendicular to the direction of force when calculating torque?

Question

According to my textbook:

Moment of a force = force $\times$ perpendicular distance of the line of action of the force from the fulcrum.

I don't understand why it would be that way (especially what mathematics goes behind it). Why is distance taken to be perpendicular to the direction of force when calculating torque, regardless of its direction?

For example, in this question:

The answer (given by the marking scheme) is supposedly $240$ $\text{N}$ $\times 1.2$ $\text{m}$ or $288$ $\text{Nm}$. The way I usually tackle questions like these would be to resolve the vector into its components and multiply the magnitude of its vertical vector with the distance.

How does the method used above by the marking scheme work? Is there a proof which shows it does?

Answer 1

The torque $\vec \tau$ by some force ${\bf \vec F}$ about a pivot is defined as $$\boldsymbol {\vec \tau}={\bf \vec r}\times {\bf \vec F}$$ where ${\bf \vec r}$ is the vector going from the pivot (or fulcrum) to the point of application of the force.

Mathematically, you know that the magnitude of the cross product of two vectors ${\bf \vec a}$ and ${\bf \vec b}$ is given as follows: $$\left|{\bf \vec a} \times {\bf \vec b}\right| = ab\sin\theta$$ where $\theta$ is the angle between the vectors (measured when vectors are tail to tail).

Therefore, you have that the magnitude of torque is $$\tau = F\underbrace{r \sin\theta}_\text{lever arm}$$

Now, because of trigonometry, you can see that $r\sin\theta$ is the $1.2 \ \rm m$ distance you highlighted. See below:

Recall that $\sin(\pi - x)=\sin x$, and you can make sense of the above, to realize that the lever arm is indeed $r\sin(\pi-\theta)=r\sin\theta$.

Answer 2

The best definition of torque is the work per unit angle of rotation that can be done by a force which is acting in a manner that would tend to cause a rotation. The work is to be done by the component of the force which is along the arc in the direction of motion. That component is perpendicular to the radius. For each small distance moved, the arc length is rθ. So the torque is $F_θ$(rθ)/θ = $F_θ$(r).

Answer 3

You want to calculate the torque about a point B due to a general force $\vec{F}$ passing through point A. Without loss of generality, decompose the force into three components ($F_1$, $F_2$, $F_3$) one of which is along the line AB.

Now treat the torque about B as the sum of the torques from the three components.

The line of action of each component is defined by the point A and the direction chosen. For $F_3$ the line of action passes through A as you can see above (by design).

This means that $F_3$ has zero torque about AB, and the total torque at B is solely due to the perpendicular components $F_1$ and $F_2$.

Mathematically this is done using a cross product which ignores any parallel components.

Also, note that you can reverse the above construct and decompose the position vector $\vec{r}_{A/B}$ along three directions, one of which is parallel to the force $\vec{F}$. In the end the parallel component will be ignored and only the perpendicular distances survive to contribute to torque. This is a bit more difficult to visualize but entirely equivalent to the first case.

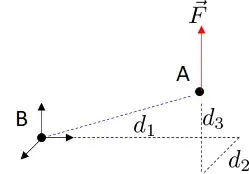
As a general rule a force vector can slide along its line of action without changing the problem at hand. In the figure above, slide the force down to meet the (1,2) plane to make the out-of-plane distance zero $d_3=0$.

It is this freedom to slide of (some) vectors that necessitate the use of perpendicular distances and cross products.

I have also posted a more general answer to the nature of torque that I recommend you read also.