Situation
Consider a supercooled liquid. If a spherical solid crystal appears, the variation of the free Gibbs energy is given by
$\Delta G = -\frac{4}{3}\pi\Delta g r^3 + 4\pi\gamma r^2$
where $\Delta g$ is considered the variation of the Gibbs energy per volume between the liquid and the solid phase, $\Delta g > 0$.
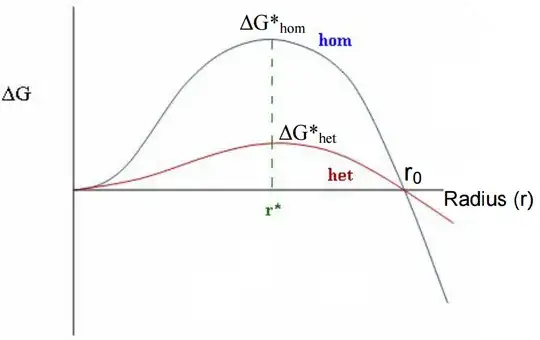
Plot of $\Delta G$:
Problem
My professor asked us to determine the critical radius at which the solid spheres become more favourable energetically and thus, the supercooled liquid begins crystallising. She meant us to find $r^*$.
I think we should rather be looking at $r_0$, since it is the variation of $G$ - only at that point does the $\Delta G$ becomes negative, which is necessary for a process to spontaneously happen.
Multiple sources treat $r^*$ as the minimum radius, but I fail to see how the maximum of $\Delta G$ would be more important that the point at which it becomes negative.
So, which one is the minimum radius the solid sphere has to grow to, in order for the liquid to solidify ?