truncation before matrix exponential: how to do it right?

Question

I'm trying to compute (numerically) the matrices of some simple quantum optical operations, which in principle are unitary. However, in my case they are unitary in an infinite-dimensional space, so I have to truncate them. The result is not necessarily unitary anymore, but if all the entries are correct up to the size that I choose, I'm happy.

So I compute the generator, truncate it to the size of my liking and then I exponentiate it, right? Nope. It doesn't work that way: the entries can be actually very wrong. In some cases they are almost correct, in some other cases they are all messed up.

Example 1: the beam splitter $\exp[i\theta(a^\dagger b + ab^\dagger)]$.

1. compute $a$ and $a^\dagger$ up to dimension (say) $m$.
2. multiply them with the kronecker product
3. exponentiate

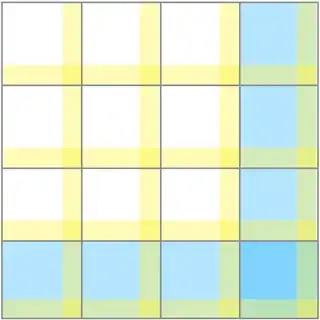
result: the entries are almost right, except for the last row and column of both spaces as in this figure (for $m=4$):

The only correct parts are the ones in the white spaces. In this case the solution is to truncate $a$ and $a^\dagger$ to size $m+1$ and then throw away the wrong rows/columns.

Example 2: the single-mode squeezer $\exp[\frac{1}{2}(z^*a^2-z{a^\dagger}^2)]$

This is all a mess: as I increase the size of $a$, the entries of the final result (which are correctly placed in a "checkerboard pattern") seem to converge to their correct values, but in order to have the first (say) 4x4 block somewhat correct I have to truncate $a$ to $m\approx 50$ and then truncate the result of the exponentiation to a 4x4 size.

Am I doing this the wrong way? Eventually I would like to produce the matrices of rather non-linear operations, where the $a$ and $a^\dagger$ operators are raised to large powers, how do I know if I'm doing it right?

UPDATE: In the first case (the beamsplitter) the unitary is in $SU(2)$, which is compact and admits finite-dimensional irreps. So I can exponentiate them individually and from those I can build the truncated unitary

In the second case (the squeezer) the unitary is in $SU(1,1)$ which is non-compact and in fact the Casimir operator has two infinite-dimensional eigenspaces: one corresponding to even and one to odd Fock states. Also for the two-mode squeezer the eigenspaces of the Casimir are infinite-dimensional (although countably infinite). So I can't use the multiplet method in this case.

Answer 1

I found the answer, at least for some of the cases that I thought were intractable, including my examples. The main tool is the disentangling theorem for the relevant group.

Example 1: the transformation is in $SU(2)$, so we need the $SU(2)$ disentangling theorem: $$ \exp(z J_+-z^* J_-) = \exp(\tau_+ J_+)\exp(\tau_ 0J_0)\exp(\tau_-J_-) $$ Here $\{J_0,J_\pm\}$ satisfy the $su(2)$ algebra relations: $[J_\pm,J_0]=\mp J_\pm,\ [J_-,J_+]=-2J_0$, and if $z=re^{i\phi}$, then $\tau_\pm=\pm e^{\pm i\phi}\tan(r),\tau_0=2\log\sec(r)$. If we apply this to the beamsplitter transformation in the form $U(\theta)=\exp[\theta(a^\dagger b-ab^\dagger)]$, we obtain $$ U(\theta) = \exp(\tan(\theta)a^\dagger b)\exp[\log\sec(\theta)(a^\dagger a-b^\dagger b)]\exp(-\tan(\theta)a b^\dagger) $$ which has no truncation issues.

Example 2: the transformation is in $SU(1,1)$, so we need the $SU(1,1)$ disentangling theorem: $$ \exp(z K_+-z^* K_-) = \exp(\sigma_+ K_+)\exp(\sigma_0K_0)\exp(\sigma_-K_-) $$ Here $\{K_0,K_\pm\}$ satisfy the $su(1,1)$ algebra relations: $[K_\pm,K_0]=\mp K_\pm,\ [K_-,K_+]=2K_0$, and if $z=re^{i\phi}$, then $\sigma_\pm=\pm e^{\pm i\phi}\tanh(r),\sigma_0=-2\log\cosh(r)$. If we apply this to the squeezing operator $S(z)=\exp[z \frac{{a^\dagger}^2}{2}-z^* \frac{{a}^2}{2}]$, we obtain $$ S(z) = \exp\left(e^{i\phi}\tanh(|z|)\frac{{a^\dagger}^2}{2}\right)\exp\left(-\log\cosh(|z|)(a^\dagger a+\frac{1}{2})\right)\exp\left(-e^{-i\phi}\tanh(|z|)\frac{{a}^2}{2}\right) $$ which has no truncation issues.

General case: in general it might be impossible to have a suitable disentangling theorem, but results like this might help approximating it (see eq. (30)-(35) for the two examples above).

I hope this will help those who will stumble upon my same issue.

Answer 2

As a practical matter, this is something where you expect the exponentiation to converge as the size of the truncated input grows. So, without knowing anything about the problem in question, I would

1. find the desired size of the answer matrix (say, $n\times n$),
2. truncate the input matrix at twice that size ($2n \times 2n$) and calculate the exponential,
3. calculate the exponential again at one larger ($[2n+1]\times[2n+1]$),
4. see if the $n\times n$ matrix has converged to the desired numerical accuracy, if it has, terminate, if not, double again, etc.

Ideally, as @Adam mentioned in a comment, you would find the eigenvectors and eigenvalues of the operator/matrix in question to do the calculation. Examining that approach is instructive in figuring out whether the above algorithm can converge. If the expression for the original operator is: $$A_{ij} = \sum_{k} V_{ki}^\star \lambda_k V_{kj},$$ then the exponential is: $$[\exp(A)]_{ij} = \sum_{k} V_{ki}^\star \mathrm{e}^{\lambda_k} V_{kj}.$$

Convergence of the second expression requires that the eigenvectors do not mix the states too widely, otherwise the sum will diverge. For example, if the eigenvalues grow linearly with $k$ then the eigenvectors have to fall faster than exponentially in $i-k$. In the ideal case, each eigenvector will have a finite number of components, guaranteeing convergence, but that may not always be the case.

Answer 3

If a matrix $A$ is not diagonal or in Jordan normal form, then you have to truncate the exponential $B=e^A$ after computing it, and not just truncate the matrix $A$ and then compute $B$. This is because the matrix elements $A_{nm}$, $n,m>N$, that you neglect by truncating $A$ to $N\times N$, are contributing to the matrix elements $B_{nm}$, $n,m\leq N$, as you can see by expanding $B=I+A+\frac{1}{2}A^2+\cdots$. The contributions to $B_{nm}$, $n,m\leq N$, from $A^2$ etc. that you neglect by truncating $A$ to $N\times N$, are $\displaystyle \sum_{k=N+1}^{\infty} A_{nk}A_{km}$, etc., which in general are not zero. What you can do is to try to compute explicitly the matrix elements $\langle n|B|m\rangle$ in the Fock basis, up to $N$. However this is not practical and can be done in limited cases, e.g. for the displacement operator $D(\alpha)=\text{exp}(\alpha \hat{a}^{\dagger}-\alpha^* \hat{a})$: $$\langle n|D(\alpha)|m\rangle=(n!/m!)^{1/2} \alpha^{m-n} e^{-|\alpha|^2/2} L_n^{(n-m)}(|\alpha|^2),$$ where $L$ are associated Laguerre polynomials (see Glauber). Unfortunately for the squeeze operator $S(\xi)$, $\xi=r e^{i\theta}$, you can easily compute only the first column and row, by using $$\langle 2n| S(\xi)|0\rangle=\frac{(-\tanh r)^n}{\sqrt{\cosh r}}\frac{\sqrt{(2n)!}}{2^n n!}e^{i n \theta},$$ $$\langle 2n+1| S(\xi)|0\rangle=0$$ for $n=0,..., N$.