Michelson interferometer beam splitter phase shift

Question

In a Michelson interferometer (image from Optics by E. Hecht ) .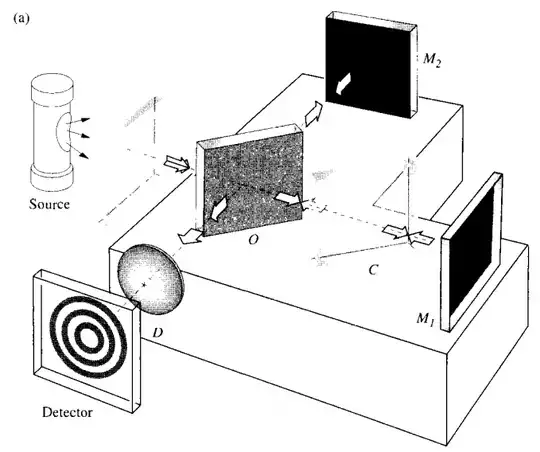

To quote from the same book:

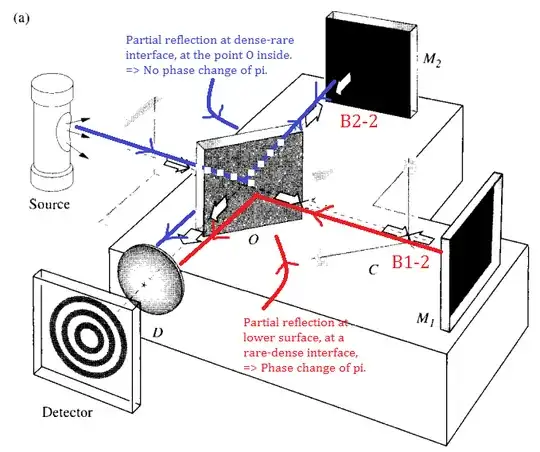
As the figure shows, the optical path difference for these rays is nearly $2d \cos 0$. There is an additional phase term arising from the fact that the wave traversing the arm $OM2$ is internally reflected in the beamsplitter, whereas the $OM1$-wave is externally reflected at $O$. If the beamsplitter is simply an uncoated glass plate, the relative phase shift resulting from the two reflections will be $\pi$ radians.

Consider a beam from $B$ from $S$ towards $O$. At $O$ it splits into two beams:

Beam B1:

1. Results from refraction of $B$ at the beam splitter $O$ towards mirror $M1$.
2. Is reflected in the opposite direction at $M1$.
3. Is reflected towards $D$ at $O$. Is it reflected before entering $O$ or after entering $O$ and encountering the air at the other side?

Beam B2:

1. Results from reflection of $B$ at the beam splitter $O$ towards mirror $M2$. Should there be a phase shift here? This is should be an air/(glass/metal coating) interface.
2. Is reflected in the opposite direction at $M2$.
3. Goes through $O$ towards detector $D$.

Question: Could someone tell me at which of these steps a phase shift occurs? It seems to me that it could happen at steps $B1-2$, $B1-3$, $B2-1$ and $B2-2$, but that is probably not right.

Answer 1

One minor detail, which is extremely important in this context, which you perhaps missed is that the beam-splitter is partially silvered at the lower surface, which implies that the appropriate location of the point O is at the lower surface of the beam-splitter (at the glass-air interface).

If we take this detail into account, the explanation is very simple:

• There are $\pi$ phase changes at steps B1-2 and B2-2, but these are common for both beams, and hence do not contribute to any net relative phase difference. (These reflections are depicted as such in the edited diagram)

• The only relative phase difference arises due to complete reflection at B1-3 (reflection at the outer, lower surface of the beamsplitter.) This occurs for only one of the two beams, not for both. Hence, net relative phase difference is $\pi$ radians. (This is represented in the diagram for the red colored beam. Note that this is not true for the other beam, shown in blue.)

• (IMPORTANT) There is no phase change of $\pi$ in the reflected beam, arising at the original division of amplitude point O, originally. This is because the division took place at the lower interface, where the interface was glass-air and not air-glass. If we invoke the Stokes' relation, you have a phase change of $\pi$ on a reflection at a rare-dense interface. This doesn't fit the description. (Hence, no phase shift of $\pi$ for the blue beam in the figure.)

Hence, the total relative phase difference between the two coherent beams, when they recombine, is only $\pi$ radians.

---

(Original image edited on suggestion by Floris).

Answer 2

The answer is the last sentence from Hecht that is quoted:

"If the beamsplitter is simply an uncoated glass plate, the relative phase shift resulting from the two reflections will be π radians."

As stated by SpeedOfLight, one reflection is from glass$\to$air (blue ray in diagram), the other from air$\to$glass (red ray).

All that is fine and good if the plate is uncoated (as Hecht assumes). However, as ProfRob comments, most partially reflecting mirrors have a thin silver coating on them (I think the one Michelson used was of this kind).

UPDATE: Actually, even for the uncoated case, I do not understand the argument of Hecht. If the plate is the same on both sides, then why would both rays reflect from the back side only? I think you need the coating to create the asymmetry.

Hence, the open question is still, what the answer would be in the case a silver-coating is present.

One then has for the blue ray a reflection glass$\to$silver, and for the red ray air$\to$silver.

I always thought reflections at metals involve a $\pi$ shift (since the tangential component of the electric field must vanish). If that were so, then for both rays you get the $\pi$ shift, so no net relative effect. Then, there is also the Fresnel equations to consider, where things depend on the polarization state, as well as the angle of incidence (if the angle exceeds Brewster, you don't get the shift anymore, or it first appears, depending on whether you go from rare to dense).

So, for the realistic scenario with a coating, I don't see a simple argument for just the $\pi$ shift. I am also inclined to think the answer should somehow depend on the value of the angle of incidence compared to the Brewster angle.

Answer 3

There is an automatic change in the phase when the wave goes ..... bounces off the mirror. Then after all that you start to play with the path lengths to introduce more phase changes.