Phase space volume and relativity

Question

Much of statistical mechanics is derived from Liouville's theorem, which can be stated as "the phase space volume occupied by an ensemble of isolated systems is conserved over time." (I'm mostly interested in classical systems for the moment.)

It's clear that special relativity doesn't change this, since relativity just adds a different set of invariances to the Hamiltonian. So under special relativity, the phase space volume of an ensemble must remain constant over time, as long as we're consistent in using a given inertial reference frame. However, this doesn't tell us how the phase space volume would change if we boosted to a different reference frame. So I'd like to know the following:

1. Can anything useful be said about how the phase space volume occupied by an ensemble of systems changes under a Lorentz boost? I guess this would entail taking a different time-slice through the system, as explained below. I would suspect that phase space volume doesn't behave very nicely under Lorentz transforms, since phase space is defined in terms of 3-position and 3-momentum.

2. If phase space volume doesn't behave nicely under Lorentz boosts, is there a generalisation (e.g. in terms of 4-position and 4-momentum) that does? And if so, where can I go to read more about it?

3. Optional bonus questions: what effect do general relativity and quantum mechanics have on all of the above?

Additional clarification

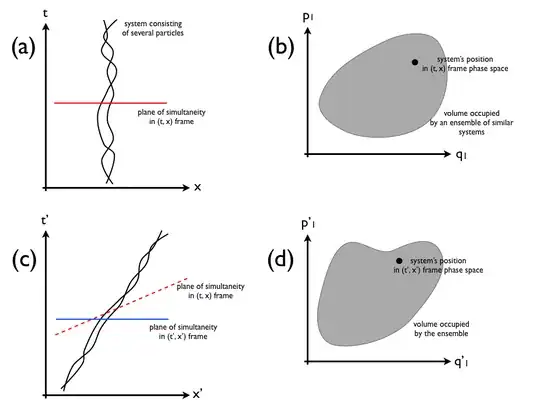
Below are some diagrams which should make it clearer what I'm asking for. (a) shows a space-time diagram of a system consisting of several classical particles. We take a simultaneous time-slice though the system (red line) and note the 3-position and 3-momentum of each particle. This gives us a point in a phase space (diagram (b)), which I've drawn as 2 dimensional for convenience. An ensemble of similar systems (meaning systems with the same dynamics but different initial conditions) can be thought of as occupying a region of this phase space. Liouville's theorem tells us that if we do the same thing at different values of $t$ (for the same ensemble of systems), the shape of this region may change but its volume will be the same.

(c) shows a Lorentz-transformed version of the same system as (a). We can take a simultaneous time-slice through the system in the new $(x',t')$ reference frame, but it will not be parallel to the one in the $(x, t)$ frame. The particles' 3-positions and 3-momenta will also be different. We can plot the system's position in the new phase space generated by doing the same procedure in the new reference frame (d). We can also plot the region of phase space occupied by the ensemble. Doing the same thing at different values of $t'$ will produce different regions with the same volume as each other. However, my question is about whether volume of the region plotted in (d) must equal the volume of the region in (b).

Progress

In this document (J. Goodman, Topics in High-Energy Astrophysics, 2012, p.12-13; unfortunately Goodman gives no further reference) there is a proof that infinitesimal phase space volumes are Lorentz invariant. It looks legit, but the author assumes that every particle's $x$ position is within the same small interval $[x, x+dx]$, which means that he doesn't have to take account of the fact that you take a different time slice when you change the reference frame. Additionally, I'm using an integrated version of Liouville's theorem, in which the ensemble has a finite rather than infinitesimal phase space volume, and it isn't immediately clear to me whether this makes a difference. So this seems to suggest that the phase space volumes sketched in figures (b) and (d) above will be equal, but I'm still not sure and would like to know where I can find the full proof, if it exists.

Further Progress

I'm awarding a 100 point bounty to Qmechanic for his helpful answer, which expresses Goodman's argument (discussed above) in more formal language. However, I don't think the question has been answered yet. This is because the argument doesn't just assume that the system occupies an infinitesimal volume of phase space. On its own this would be fine, since you can just integrate over phase space to get the finite phase-space volume version. The problem is that this argument also assumes the system occupies only an infinitesimal volume of real space. In general, a system that occupies an infinitesimal volume of phase space can occupy a finite area of actual space (think of a system composed of multiple, spatially separated, classical particles, as illustrated above) and so this argument seems to cover only a restricted subset of the cases I'm interested in. Goodman's argument is fine if you're considering non-interacting particles or fluids in equilibrium (which makes sense given its origins in astrophysics) but I'm also interested in multi-particle systems that may or may not be in thermal equilibrium. It is my strong intuition that the argument can be extended to deal with all cases, and I'll happily award an additional 100 point bounty to anyone who can show how to do so.

I think one route to an answer might be to note that, in special relativity, classical particles cannot interact unless they actually collide. This probably means that in the times in between collisions they can be thought of as occupying their own individual phase spaces after all, and perhaps with the aid of the proof that's been presented and some careful accounting about what happens during collisions, it will all work out OK. But of course then it has to be extended to deal with (classical) fields, which could be tricky. One gets the feeling there ought to be a nice simple way to derive it from Lorentz invariance of the Lagrangian, without worrying about what type of system we're dealing with. (I'll award a 200 point bounty to a satisfactory answer that takes this latter approach!)

Answer 1

I) Let us here prove the invariance of the two $3$-forms

$$ p^0 dq^1 \wedge dq^2 \wedge dq^3\qquad \text{and}\qquad \frac{dp_1 \wedge dp_2 \wedge dp_3}{p^0} \tag{1} $$

under (restricted) Poincare transformations. As a consequence, the volume-form

$$\Omega~:=~\frac{1}{3!}\omega\wedge \omega\wedge\omega~=~ dp_1 \wedge dp_2 \wedge dp_3 \wedge dq^1 \wedge dq^2 \wedge dq^3 \tag{2}$$

is also an invariant, where

$$ \omega ~:=~\sum_{i=1}^3 dp_i \wedge dq^i \tag{3}$$

is the symplectic 2-form.

Let's work in units where the speed of light $c=1$ is one. Here we will assume:

1. The metric is $\eta_{\mu\nu}={\rm diag}(-1,+1,+1,+1)$.

2. The $q^{\mu}=(t, {\bf q})$ and $p^{\mu}=(p^0, {\bf p})$ transform under Poincare transformations as an affine and a linear $4$-vector, respectively.

3. All particles have the same rest-mass $m_0\geq 0$. In particular, the energy is

$$ p^0 ~=~ \sqrt{{\bf p}^2+m_0^2 }.\tag{4}$$

4. The momentum is kinetic

$${\bf p}~=~p^0{\bf v}.\tag{5}$$

Since the two $3$-forms (1) are clearly invariant under translation and rotations, it is enough to consider a Lorentz-boost along the $q^1$-axis. This follows because

$$ p^{0}dq^1, \qquad dq^2, \qquad dq^3, \qquad \frac{dp_1}{p^0},\qquad dp_2,\qquad dp_3,\tag{6} $$

are all invariant under boost along the $q^1$-axis. E.g. the fourth item

$$\frac{dp_1}{p^0}~=~\frac{d\overline{p}_1}{\overline{p}^0}.\tag{7}$$

on the list (6) is invariant because

$$ \frac{\partial \overline{p}_1}{\partial p_1 } ~=~ \frac{\partial [\gamma(p_1-\beta p^0)]}{\partial p_1 } ~\stackrel{(4)}{=}~ \gamma(1-\beta \frac{p^1}{p^0}) ~=~ \frac{\gamma(p^0-\beta p_1)}{p^0} ~=~ \frac{\overline{p}^0}{p^0}, \quad \gamma~:=~(1-\beta^2)^{-1/2}.\tag{8}$$

Only the invariance of the first item

$$p^{0}dq^1~=~\overline{p}^{0}d\overline{q}^1\tag{9}$$

on the list (6) is non-trivial, so let us concentrate on that one.

Proof of eq. (9). The derivation essentially follows Ref. 1. Consider an arbitrary fixed point $({\bf q}_{(0)},{\bf p}_{(0)})\in\mathbb{R}^6$ in phase space at $t=t_{(0)}=\overline{t}_{(0)}$. Because of translation symmetry, we may assume that the point ${\bf q}_{(0)}=\overline{\bf q}_{(0)}$ is a common origin for the two coordinate systems (one barred and one un-barred) of the Lorentz transformation at $t=t_{(0)}=\overline{t}_{(0)}$. Let us define

$$ {\bf x}(\Delta t)~:=~{\bf q}(t)-{\bf q}_{(0)}, \qquad \Delta t~:= t-t_{(0)}, \tag{10}$$

and

$$ \overline{\bf x}(\overline{\Delta t})~:=~\overline{\bf q}(t)-\overline{\bf q}_{(0)}, \qquad \overline{\Delta t}~:= \overline{t}-\overline{t}_{(0)}. \tag{10'}$$

We imagine that we observe an infinitesimally small space-time (and energy-momentum) region around the fixed point $(q^{\mu}_{(0)},p^{\nu}_{(0)})\in\mathbb{R}^8$. Since we are only interested in first-order variations in positions, it is enough to work to zero-order variations in momenta. In other words, we can imagine all particles travel with the same constant energy-momentum $p^{\mu}=p^{\mu}_{(0)}\in\mathbb{R}^4$ (and velocity ${\bf v}={\bf v}_{(0)}\in\mathbb{R}^3$). Then

$$ {\bf x}(\Delta t)~=~{\bf v}\Delta t+ {\bf x}_0 ,\qquad {\bf v}~=~\frac{{\bf p}}{p^0}, \tag{11}$$

and $$ \overline{\bf x}(\overline{\Delta t})~=~\overline{\bf v}\overline{\Delta t}+ \overline{\bf x}_0,\qquad \overline{\bf v}~=~\frac{\overline{\bf p}}{\overline{p}^0}. \tag{11'}$$

The Lorentz transformation reads

$$ \overline{\Delta t} ~=~\gamma(\Delta t-\beta x^1(\Delta t)), \qquad \overline{x}^1(\overline{\Delta t}) ~=~\gamma(x^1(\Delta t)-\beta \Delta t), $$ $$ \qquad \overline{x}^2(\overline{\Delta t}) ~=~x^2(\Delta t), \qquad \overline{x}^3(\overline{\Delta t})~=~x^3(\Delta t), \tag{12}$$

and

$$\overline{p}^0~=~\gamma(p^0-\beta p_1) , \qquad \overline{p}_1~=~\gamma(p_1-\beta p^0), \qquad \overline{p}_2~=~p_2, \qquad \overline{p}_3~=~p_3 .\tag{13}$$

Eqs. (11) and (11') can only both hold if the following well-known relativistic formulas hold

$$ \overline{v}^1~=~\frac{v^1-\beta}{1-\beta v^1}, \quad \overline{v}^2~=~\frac{v^2}{\gamma(1-\beta v^1)},\quad \overline{v}^3~=~\frac{v^3}{\gamma(1-\beta v^1)}, \quad\text{(rel. velocity addition)}\tag{14} $$

and

$$ \overline{x}^1_0~=~\frac{x^1_0}{\gamma(1-\beta v^1)}, \quad \overline{x}^2_0~=~x^2_0+\frac{\beta v_2x^1_0}{1-\beta v^1} , \quad \overline{x}^3_0~=~x^3_0+\frac{\beta v_3x^1_0}{1-\beta v^1}, \quad \text{(length contr.)}. \tag{15} $$

On the other hand the first eq. in (13) yields

$$ \frac{\overline{p}^0}{p^0} ~=~\gamma(1-\beta v^1). \tag{16}$$

Combining the above equations yields eq. (9): $$ x^1_0 p^0~=~\overline{x}^1_0 \overline{p}^0. \tag{17}$$

$\Box$

II) Comments:

1. Part I discusses the local Poincare invariance. An integrated version therefore also exists (with appropriate change of integration regions under Poincare transformations).

2. Part I concerns systems consisting of particles of a single kind only. The generalization to mixtures is e.g. partially discussed in Ref. 2.

3. A similar proof as in part I shows that the symplectic $2$-form (3) is invariant under restricted Poincare transformations.

References:

1. J. Goodman, Topics in High-Energy Astrophysics, 2012, p.12-13.
2. S. R. de Groot, W. A. van Leeuwen and Ch. G. van Weert, Relativistic kinetic theory, 1980.

Answer 2

EDIT: Upon thinking about it a bit, i am no longer sure this proof is actually correct. Nonetheless I'll leave this answer up for bookkeeping until I figure it out.

---

Here is a rather simple proof. We first make some assumptions:

1. The momentum $\mathbf p$ and the Hamiltonian $H(\mathbf x,\mathbf p,t)$ behave as a four-vector together under a Lorentz transformation, i.e. as $$ p^\mu=(H,\mathbf p). $$
2. Since invariance under rotations and translations is obvious, it is sufficient to consider only boosts in one spatial direction. Hence I will work with a two dimensional spacetime with coordinates $(t,x)$ ($c=1$)

A Lorentz transformation then has the form $$ \left(\begin{matrix} t^\prime \\ x^\prime\end{matrix}\right)=\left(\begin{matrix}\cosh(\phi) & -\sinh(\phi) \\ -\sinh(\phi) & \cosh(\phi)\end{matrix}\right)\left(\begin{matrix} t \\ x\end{matrix}\right), $$ and the same is true with $t$ and $x$ replaced by $H$ and $p$ respectively. In particular, since the Hamiltonian is a function, this means $$ H^\prime(x^\prime,p^\prime,t^\prime)=\cosh(\phi)H(x,p,t)-\sinh(\phi)p \\ p^\prime=\cosh(\phi)p-\sinh(\phi)H(x,p,t) \\ t^\prime=\cosh(\phi)t-\sinh(\phi)x \\ x^\prime=\cosh(\phi)x-\sinh(\phi)t. $$

We need to prove that Lorentz transformations are canonical. To that end we use the odd-dimensional formulation of Hamiltonian dynamics. Phase space has the coordinates $(x,p,t)$, and the Poincaré-Cartan form is $$ \theta=pdx-H(x,p,t)dt. $$ We use the extended definition of canonical transformations, whereby the transformation $$ x^\prime=x^\prime(x,p,t) \\ p^\prime=p^\prime(x,p,t) \\ t^\prime=t^\prime(x,p,t) $$ is canonical if $$ \theta^\prime=p^\prime dx^\prime-H^\prime(x^\prime,p^\prime,t^\prime)dt^\prime=\theta+dW $$for some function $W$.

Inserting the Lorentz transformation explicitly gives $$ \theta^\prime=\left(\cosh(\phi)p-\sinh(\phi)H\right)\left(\cosh(\phi)dx-\sinh(\phi)dt\right) \\ -\left( \cosh(\phi)H-\sinh(\phi)p \right)\left(\cosh(\phi)dt-\sinh(\phi)dx\right) \\ =pdx-Hdt=\theta, $$ i.e. the Poincaré-Cartan form is invariant, thus Lorentz transformations are canonical.

We are essentially done, but to show the invariance of volume more explicitly, the symplectic potential (canonical $1$-form) for a hypersurface $\sigma:\Sigma\rightarrow P$ ($P$ is the odd-dimensional phase space) is $$ \theta_\Sigma=\sigma^\ast\theta, $$ and the symplectic form is $$ \omega_\Sigma=d\theta_\Sigma. $$ Since the equal-time phase space is two dimensional, the symplectic form is the Liouville volume form.

The equal-time phase space for the unprimed observer is given by $t=c$, while the equal-time phase space for the primed observer is $t^\prime=c$. We obtain for the symplectic forms $$ \theta_{t=c}=pdx,\quad \omega_{t=c}=d\theta_{t=c}=dp\wedge dx, $$ and $$ \theta_{t^\prime=c}=p^\prime dx^\prime,\quad \omega_{t^\prime=c}=d\theta_{t^\prime=c}=dp^\prime\wedge dx^\prime, $$ which are of the same form, therefore the phase space volume is Lorentz invariant.

Answer 3

Phase space is Lorentz invariant. You can prove this by writing an integral over $d^4$ x $d^4$ p and doing a Lorentz transformation, but there's a nice short proof in Padmanabhan's book "Gravitation", p.26 :

For an observer moving with four-velocity $u_i$, the proper three-volume element is given by $d^3V = u_0d^3x$ which is a scalar invariant. To prove this, note that the quantity $d^4V = dx \ dy \ dz \ dt$ is a scalar. Multiplying this by $1 = u_0\frac{d\tau}{dt}$ and noting that $d\tau$ is invariant, we conclude that $d^3V = u_0d^3x$ is an invariant.