5

When we describe the interaction between two-level atom and single-mode electromagnetic field in quantum optics, we have the so-called Rabi-model before the rotating-wave approximation, by which the Rabi-model becomes the Jaynes-Cummings model. In the Rabi-model, there are the counter-rotating terms, which are absent in the Jaynes-Cummings model, proportional to $\hat{\sigma}_{-}^{\dagger}\hat{a}^{\dagger}$ or $\hat{\sigma}_{-}\hat{a}$.

Do these terms violate the energy conservation? Are they physical operator? How can we understand the time-evoltuion of the system with those operation?

Veteran
  • 675
  • 5
  • 11

2 Answers2

3

Yes, these terms $\hat\sigma_{+}\hat{a}^\dagger$ and $\hat\sigma_{-}\hat{a}$ does not conserve energy. The physical meaning of these operators are given below

$\hat\sigma_{+}\hat{a}^\dagger$ corresponds to emission of a photon as the atom goes from the ground state to excited state.

$\hat\sigma_{-}\hat{a}$ corresponds to absorption of a photon as the atom goes from excited state to ground state.

As you could see atoms only goes to excited state by absorbing a photon and comes back to ground state by emitting a photon. These two operators tells us the opposite thing, so it does not make any sense, so it can not be physical operators.

The evolution of atomic ladder operator goes like photon ladder operators i.e, $\sigma_{\pm}(t)=\sigma_{\pm}(0)\exp(\pm i \omega_{0}t)$

So the product of two operators evolves as

$$\hat\sigma_{+}\hat{a}^\dagger \approx \exp[i(\omega_{0}+\omega)t]$$

$$\hat\sigma_{+}\hat{a}^\dagger \approx \exp[-i(\omega_{0}+\omega)t]$$

As you may surprised to see the above two expressions has terms $(\omega_{0}+\omega)$ . These terms are rapidly oscillating terms which we drop while making Rotating Wave Approximation. This is the same reason we are also dropping these terms in the Jaynes-Cumming's Model Hamiltonain as well.

FearlessVirgo
  • 646
3

Interaction terms $H_\mathrm{int}$ in the Hamiltonian induce state-to-state transitions at some random moments of time. Considering the time evolution of the system, for example, by means of S-matrix $$ \hat{T}\exp\left\{-\frac{i}\hbar\int\limits_0^t H_\mathrm{int}(t')dt'\right\}=\sum_{n=0}^\infty\left(-\frac{i}\hbar\right)^n\int dt_1\ldots dt_n\:\hat{T}H_\mathrm{int}(t_1)\ldots H_\mathrm{int}(t_n), $$ we need to take into account actions of all terms in $H_\mathrm{int}$ at all possible moments of time from 0 to $t$ in all possible orders.

So if we have some terms in the Hamiltonian corresponding to photon absorption and emission, we need to take into account occurrence of the corresponding processes during the time evolution in all possible orders. In particular, if we allow first atomic de-excitation $\sigma_-$ and then excitation $\sigma_+$ (see top part of the picture), we automatically should allow the reverse order: first atomic excitation $\sigma_+$ and then de-excitation $\sigma_-$ (bottom part of the picture). In each of these processes we can absorb $a$ (if present) or emit $a^+$ the photon, I have drawn only the simplest examples where the photon number is zero both in the beginning and in the end. It is quite general property of quantum field theory that if two any interaction processes can occur in the direct order, then they can occur in the reverse order as well (of course, not always with quantitatively same effects), if particle occupation numbers allow it.

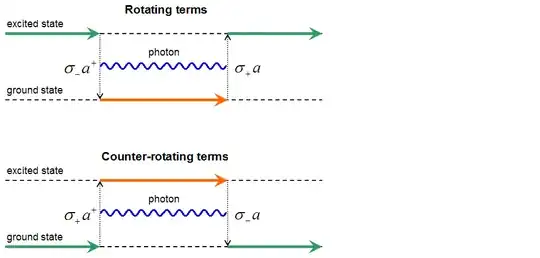
enter image description here

As concerns energy conservation: it is the property of total time-independent Hamiltonian. It is not the property of its separate terms like $a^+a$ or $\sigma_-a^+$. However in the perturbation theory formalism we can treat "energy conservation" in the following sense: is the sum of single-particle energies (atom energy + photonic field energy) the same before and after the interaction? In other words: does the specific interaction term commute with the noninteracting part $H_0$ of the Hamiltonian? It is quite obvious that answer is no, there is no such requirement for the interaction terms that they should commute with $H_0$.

Indeed, in this sense both rotating and counter-rotating terms violate "energy conservation", except when atomic transition energy is exactly equal to the photon energy (it is not general case). Of course, near the resonance the "energy non-conservation" induced by rotating terms is much smaller than that induced by counter-rotating ones, this is why the role of rotating terms in time evolution is much more significant, but this difference is only quantitative.

Alexey Sokolik
  • 2,453