Does the Lorentz invariance of Maxwell's equations apply here?

Question

Relativity and Current in Wire

The question here, (which wasn't answered properly) asks why the electron density of a current carrying wire does not increase. If it does, why is there no force on the charge? My heuristic estimate of Lorentz transformations says that the electric field of the electrons should also increase.

Extensive online research has led me to only two legitimate answers to the question posted in the link. The first is simply to state the fact that electrons and protons have the same density throughout the wire as a definition. The second is to say that since electrons are free to move, any electric field in the lab frame can easily be cancelled out by the freely moving electrons if they move apart (becoming more spaced out). In this case, there is no disagreement between Maxwell's equations and the Lorentz transformed Maxwell's equations.

But surely we can just engineer a wire in which the electrons are not free to change their spacing, but only move in the forward direction? Then the Lorentz transformed solution for the acceleration of the particle disagrees with the classical results? I was not satisfied by the explanations given as they were not fundamental enough. How do we resolve this?

Answer 1

The question you linked to is confusingly worded, and I'm not sure if I understand it. We start by assuming that in the lab frame, you see moving electrons and stationary protons at the same charge density, so that the wire appears neutral. There are several possible situations, and I'm not sure which one you're getting at:

1) If you now boost to a frame in which the electrons are stationary and the protons are moving, what do you see? The answer is that the proton density gets Lorentz contacted and appears to increase, while the electron density no longer gets Lorentz contracted and appears to decrease. In this frame, the charge densities no longer balance out, and the wire appears to have a net positive charge.

2) If you stay in the lab frame and slowly turn down the battery's voltage, but leave the wire connected to it, then the electrons will slow down and their charge density will appear to decrease, which would lead to a net positive charge on the wire, but the wire draws additional electrons from the battery and remains neutral - so you're adding external electrons into the system. (The battery has one terminal grounded, and therefore acts as an infinite sink or source of electrons as needed - see http://www.colorado.edu/physics/phys3320/phys3320_sp12/AJPPapers/AJP_E&MPapers_030612/Gabuzda_RelMagneticForce.pdf for a discussion.)

3)(a) If you instantaneously cut the wire's connection to the battery completely, without giving it time to equilibrate, then at first the electrons will appear to keep moving and begin to pile up at one end of the wire. This pile-up will lead to a net charge imbalance. Since the wire is a conductor, some electrons will be repelled by the excess negative charge toward which they are moving and reverse direction. Eventually the electrons will all settle down, and the wire will have a net positive charge.

3)(b) Same as (3)(a), but your wire is not a conductor and magically only allows electrons to move in one direction. In this case the negative charge piles up and one end of the wire, and you end up with a net charge gradient along the wire. (The exact distribution depends on the rules under which your magical wire works.)

Answer 2

Does the Lorentz invariance of Maxwell's equations apply here?

Yes. Lorentz invariance is pretty universal. The "laws of physics" don't change when you and your laboratory go from being at rest to a state of uniform motion.

Relativity and Current in Wire

The issue with that is the length-contraction explanation for the magnetic field around the wire is wrong. See this question where I asked about it.

The question here, (which wasn't answered properly) asks why the electron density of a current carrying wire does not increase.

It doesn't increase, because the drift velocity is miniscule. See Wikipeda where there's a worked example: "Therefore in this wire the electrons are flowing at the rate of −0.000023 m/s."

If it does, why is there no force on the charge? My heuristic estimate of Lorentz transformations says that the electric field of the electrons should also increase.

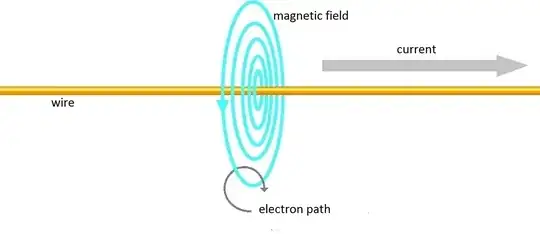
There is a rotational magnetic force on a charged particle near the wire. The test electron moves in a near-circular fashion. It doesn't do this because the wire is negatively charged.

Extensive online research has led me to only 2 legitimate answers to the question posted in the link. The first is simply to state the fact that electrons and protons have the same density throughout the wire as a definition. The second is to say that since electrons are free to move, any electric field in the lab frame can easily be cancelled out by the freely moving electrons if they move apart (becoming more spaced out). In this case, there is no disagreement between Maxwell's equations and the lorentz transformed Maxwell's equations.

IMHO the point to appreciate is that we're dealing with electromagnetic fields here, and electromagnetic field interactions result in linear electric force and/or rotational magnetic force. See what Minkowski said Space and Time:

"In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect".

The electron has an electromagnetic field, not an electric field. Ditto for the proton, or the positron. When you place an electron and a positron down with no initial relative motion they move directly towards one another. The force is linear. However when you throw the electron past the positron there's a rotational force too, see positronium. Like Minkowski said there's two forces, with a "screw" relationship. In the current-in-the-wire the linear forces balance but the rotational forces don't, because the electrons are moving. So that test electron moves in a near-circular fashion.

But surely we can just engineer a wire in which the electrons are not free to change their spacing, but only move in the forward direction? Then the Lorentz transformed solution for the acceleration of the particle disagrees with the classical results? I was not satisfied by the explanations given as they were not fundamental enough. How do we resolve this?

By properly understanding how a magnet works.