$\phi^{4}$ Propagator - Feynman Diagram: internal vertex that loops back to itself

Question

In all that follows I'll be dealing with everything massless.

The free, massless propagator ($\mathcal{L} = \int d^{4}x \left(\partial \phi(x) \right)^{2} $) is supposedly given by $G_{0}(x,y) = c (x-y)^{-2}$, where I believe $c = \frac{1}{4\pi^{2}}$.

I'm trying to calculate the propagator in $\phi^{4}$-theory, specifically the contribution due to this diagram:

Using the Feynman rules in position space, I believe that I should be getting a contribution of the form: $$ C(x_{1},x_{2}) = -i\lambda \int d^{4}u\ G_{0}(x_{1}, u) G_{0}(u,u) G_{0}(u,x_{2}) $$

However, here is my question: why do I get $G_{0}(u,u) = c (u-u)^{-2} = \mathrm{undefined}$? There's no way I can see to evaluate this integral.

How do I deal with this? Maybe I've got the wrong order of variables? I'm new to these kinds of calculations.

Answer 1

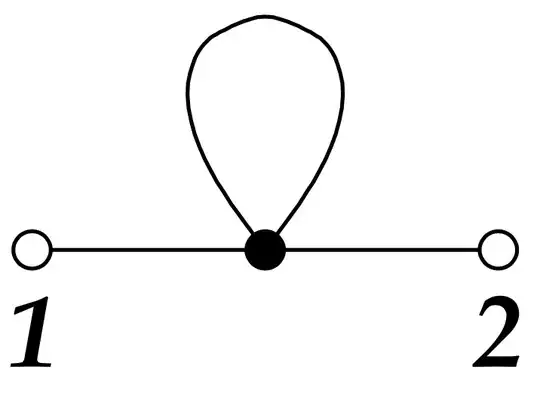
To define a $\phi ^4$ massless theory, you can't simply start from a lagrangian $$\mathscr L = \frac{1}{2}(\partial\phi)^2-\frac{g_0}{4!} \phi^4,$$ separate a kinetic term $\mathscr L _0= \frac{1}{2}(\partial\phi)^2$ and do perturbation theory around $g _0=0$. The reason is that, even in lowest order of perturbation theory, the $\phi^4$ term will give rise to divergent diagrams like the one you have just calculated, which are formally infinite. To treat such diagrams, you need:

1. To introduce a regulator, like an UV cutoff $\Lambda$ in the propagators.
2. To impose some (in this case, three) finiteness conditions on the Green's functions.
3. To express all quantities in terms of the (finite) parameters introduced in step 2.

The procedure will work only if you start from a renormalizable lagrangian like: $$\mathscr L = \frac{1}{2}(\partial\phi)^2-\frac{m_0^2}{2}\phi^2-\frac{g_0}{4!} \phi^4.$$

The purpose of Step 1 is to make sense of divergent quantities like $G_0(x-x)$. A simple way that works for the $\phi^4$ theory is Pauli-Villars regularization: $$\tilde G_0(p)=\frac{1}{p^2-m_0^2+i\varepsilon}\to \tilde G_0(p)_\Lambda = \frac{1}{p^2-m_0^2+\frac{(p^2)^2}{\Lambda^2}+\frac{(p^2)^3}{\Lambda^4}+i\varepsilon}.$$

In step 2 we can at one time make the theory massless and eliminate the divergent diagram that you have calculated. We simply require that$^1$: $$\tilde G(p^2=0)^{-1}=0.$$ This ensures that the physical mass of the particles described by the theory is zero, and if you calculate the propagator to first order in $g_0$, you'll also find that the constant value of the divergent diagram is exactly canceled by the bare mass $m_0^2$.

---

$^1$ Actually, to first order in $g_0$, this condition suffices to renormalize the theory.

Answer 2

I have just tried to compute this diagram in momentum space and I think it gives a zero contribution in the massless case. Basically this is because within the loop you will get an integral like $$ \int \frac{\mathrm d^4 k}{(2\pi)^4} \frac{\mathrm i}{k^2 - m^2 + \mathrm i \epsilon} \,,$$ where $m = 0$. One professor said that this integral will give zero because for $m = 0$, there is no mass/energy scale that this loop integral could probe. I remember that the explanation did not satisfy me at the time, I unfortunately do not have a better one right now.

Then also with loops, it is not uncommon for those to give infinities. This will lead to regularization and eventually to renormalization which feels like Pandora's box. Your integral seems to diverge since there are eight powers of $u$ in the numerator (from the integration measure) but only six powers in the denominator (from the Green's functions). It might still be infinite. Then you have to go to momentum space and use dimensional regularization.

I can give you momentum space derivation of this tadpole diagram with dimensional regularization that I did a couple years ago as a homework assignment in the QFT class I took. You can download the original and reviewed PDF to read it in full. This is the excerpt:

The final result is proportional to $m$. Setting $m = 0$ will make this while thing vanish, therefore the result seems to be zero in the massless theory.