0

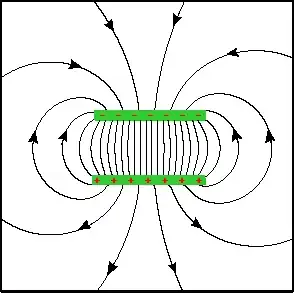
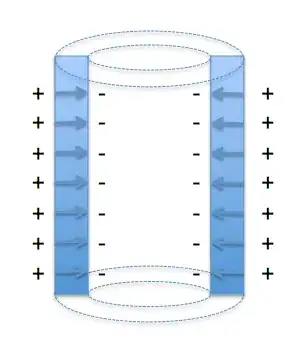
A cylindrical capacitor (two circular metal plates in vacuum) creates an electric field profile. As a thought experiment, can I set up currents to make a magnetic field which completely matches this profile inside the cylinder?

The currents can be placed anywhere (e.g, outside the cylinder with 3D complexity), but I'd prefer to have divergent-free currents, so that all fields are static. To be clear, magnetic monopoles are not allowed (the reverse problem of coverting a solenoid's magnetic field is easily solved by placing electric monopoles on the cylindrical boundary).

field

bobuhito
  • 1,046
  • 1
  • 8
  • 16

2 Answers2

1

This can be done by finding the charge density on the plates and then mimicking it with solenoids from infinity. This probably therefore amounts to circular currents above the top plate (extending infinitely above the top plate) and the mirrored currents below the bottom plate.

I was really hoping for a solution which does not require infinite volume, so await more answers or a proof that infinite volume is required.

Community
  • 1
bobuhito
  • 1,046
  • 1
  • 8
  • 16
0

No, you can't do this. The explanation is that the electric field lines will "stop" on the inner boundary; magnetic field lines have to be continuous, so somewhere inside the cylinder these lines would be traveling "up and out" to form closed lines of flux. This is the approximate distribution of field lines in the capacitor:

enter image description here

For a magnet, those arrows don't stop at the -ve charged plate.

Floris
  • 119,981