Charge distribution on a plate of Capacitor with Dielectrics .

Question

I had this Homework Problem with a capacitor (parallel plate) that has a group of 3 dielectrics between it like so :

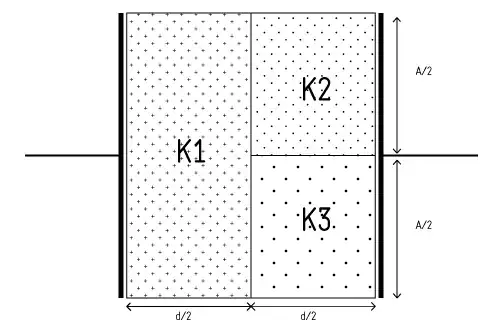
Now We were asked to find the equivalent capacitance and the distance of separation between the plates was $d$ and its area was $A$.

Now i assumed that the 3 individual dielectrics would act as individual capacitors and K2 would be parallel to K3 and their resultant series with K1

This was also the method I found in many other books.

$$C_{k1}~=~ \frac{2K_1\epsilon_oA}{d} $$ $$C_{k2}~=~ \frac{K_2\epsilon_oA}{d}$$ $$C_{k3}~=~ \frac{K_3\epsilon_oA}{d}$$

Finally $$C_{2,3}= \frac{K_2\epsilon_oA}{d} + \frac{K_3\epsilon_oA}{d} \implies \frac{(K_2+K_3)\epsilon_oA}{d}$$

And $$C_{(2,3),1} = \frac{\frac{(K_2+K_3)\epsilon_oA}{d}.\frac{2K_1\epsilon_oA}{d}}{\frac{(K_2+K_3)\epsilon_oA}{d}+\frac{2K_1\epsilon_oA}{d}}$$

Our teach told us that the answer was incorrect , When I told him about the books he told us that the books had it all wrong. So I asked him for the solution .

He divided the First Dielectric Into two parts along the line joining the bisector of area :

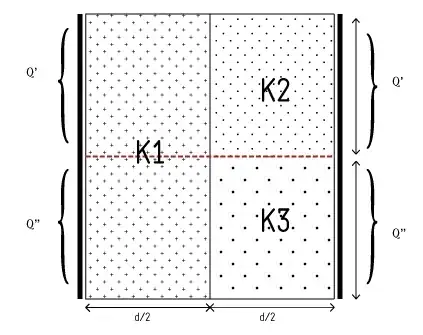
And Did the shown Charge distribution.

Later he equated the potentials and stuff like so

$$V_{Q'_1,Q'_2}=\frac{Q'd}{K_1\epsilon_oA}+\frac{Q'd}{K_2\epsilon_oA}~~~~....1$$ $$V_{Q''_1,Q''_3}=\frac{Q''d}{K_1\epsilon_oA}+\frac{Q''d}{K_3\epsilon_oA}~~~~....2$$

then said that $V_{Q'_1,Q'_2}=V_{Q''_1,Q''_3}$ he then put the values of $Q',Q''$ in the equation $$C=\frac{Q'+Q''}{V}$$

Basically getting a result that was quite different from the result given in books .

• I asked him how a single plate , the one in contact with the K1 dielectric could have Two different charges on the same surface.
• He told me that it was because of the accompanying dielectrics
• Was my question valid the first point ?
• Whose solution is correct?

Answer 1

Your professor is right. Capacitors K2 and K3 are not parallel and then in series with capacitor K1, because the vertical line that is separating K1 on left and K2 and K3 on right is not an equipotential line. That is, potentials on the left side of K2 and on the left side of K3 are not the same!

You actually have upper half of K1 and K2 in series and lower half of K1 and K3 in series, all together parallel.

Interesting note: only if you've put a metal plate between K1 on the right and K2 and K3 on the left, your procedure would be right!

Answer 2

As Pygmalion points out, the flaw in your reasoning is assuming that the surface of the $K_1$ dielectric is an equipotential, which it need not be. At the triple junction there will be some accumulation of charge and the accompanying electric fields, which will result in a potential difference between the two sides of dielectric 1's surface.

Let me explain how the different charges $Q'$, $Q''$ on the plate come about. Any dielectric inside a capacitor gets polarized, to some amount that is determined by its susceptibility. In a uniform electric field, this polarisation does not cause charge build-up in the bulk of the dielectric but it does cause an excess of charge on the surface. This puts a layer of positive charge on the negative plate of the dielectric (and vice-versa). This in turn "damps" the net charge seen by the electric field, which is correspondingly lower and makes for a lower voltage, thus increasing the capacitance.

When you have two different dielectrics in contact with the same plate, the dielectric-surface charges will be different, but the main principle is that the total charge density (i.e. on the metal plus the dielectric) is the same in both sections. The situation would be the same if the two dielectrics were separate (i.e. cutting the diagram along the red dashed line): you need the total charges, which determine the electric field and therefore the voltage, to match.

On the whole then: there's different charges on the metal and on the dielectric (i.e. "his distribution"), but the total charge density is the same.

This is sufficient to determine the total capacitance, so his expression for that is correct.

I don't think, however, that the charges on the plate on the left are distributed like that, though. If you cut along the red line, it will definitely get distributed like that. If you bring the two halves together, since the 1-2 and 1-3 junctions are not at the same potential, you'll see some rearrangement of charges and a fairly complicated, nonuniform electric field (since the problem has lost its vertical translation invariance); this may even bring about bulk charges in some sections of the capacitor. The charge distribution on the left plate, and thus on the neighbouring dielectric, will probably be quite complicated. However, the capacitance will not change since the two halves of the left plate were at the same potential.