Can an object *immediately* start moving at a high velocity?

Question

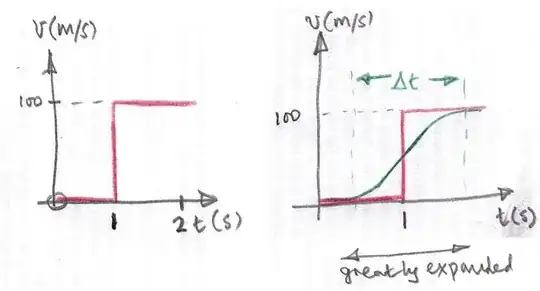
What I mean is, suppose a ball is fired from a cannon. Suppose the ball is moving at 100 m/s in the first second. Would the ball have started from 1m/s to 2m/s and gradually arrived at 100m/s? And is the change so fast that we are not able to conceive it? Or does the ball actually start its motion at 100m/s as soon as the cannon is fired?

Suppose a 40-wheeler is moving at the speed of 100 kmph. And it collides with a car and does not brake (The car is empty in my hypothesis ;-) ). If a body does not reach a certain speed immediately and only increases speed gradually, does that mean that as soon as the truck collides with the car, the truck momentarily comes to rest? Why I ask this is because the car is not allowed to immediately start at the truck's speed. So when both of them collide, the car must start from 0 to 1kmph to 2kmph and finally reach the truck's speed. Does this not mean that the truck must 'restart' as well? Intuition tells me I'm wrong but I do not know how to explain it physically being an amateur.

When is it possible for a body to accelerate immediately? Don't photons travel at the speed of light from the second they exist?

Answer 1

The answer to your question is "No" as this would require an infinite acceleration and hence an infinite force to be applied.
However to simplify problems it is sometimes convenient to assume an instantaneous jump in velocity as in the left hand graph.

It might be that the actual change in velocity is as per the green line in the right hand graph but because the change in velocity $\Delta t$ takes place over such a short period of time, perhaps $\Delta t \ll 1$ in this example, the approximation to an "instantaneous" change has little bearing on the final outcome.

So every time you see a velocity against tine graph with some sort of "corner", where a gradient (= acceleration) cannot be found, you have to think that the corner is actually rounded but that rounding occurs over a very short period of time compared with the time scale of the whole motion it matters not a lot.

Another example is of problems where a ball rebounds from the ground and you have to find the time it takes to reach a certain height after the rebound.
It is unlikely that you consider the time that the ball is in contact with the ground and slowing down with an acceleration much greater than $g$ (acceleration of free fall) stopping and then initially accelerating upwards at an acceleration greater than $g$.
Usually the sums are done assuming that the acceleration is $g$ all the time because the time that the ball is in contact with the ground is so much smaller than its time of flight through the air.

Answer 2

To answer this, one must understand how motion starts. The motion of the canon-ball starts due to force applied on it. The force directly does not lead to a high velocity. Force leads to acceleration, ie, change in velocity. So, the motion is dictated by

$$F=ma=m\dfrac{\mathrm dv}{\mathrm dt}$$

The change in velocity $\mathrm dv$ during the first moments (which is the question) depends on the infinitesimal time period $\mathrm dt$ you are considering. This time period can be arbitrarily small, and as the force $F$ is fixed, the change in velocity $\mathrm dv$ can be arbitrarily small too. So yes, the motion starts 'gradually', which is to say that the ball doesn't have $0$ velocity and then $100\ \mathrm{m/s}$ without reaching a velocity in between.

Note: We should technically be talking about changes in momentum, instead of velocity. If one adds quantum and relativity to the picture, the analysis becomes more complicated, and the question itself has no meaning in that scenario. I assume you only wanted to know about everyday 'canon-ball' situations.

Answer 3

Nothing propagates instantly

For starters, any real object has a non-zero size. If you apply force to one side of a cannonball, it will start moving before the other side of the cannonball can be affected by that force. The time will be very small ("so fast that we are not able to conceive it") but nonzero. The cannonball will experience some compression, and in general (for reasonable energies) the propagation will be limited by the speed of sound in that material.

So even without even going to gradual acceleration (the main purpose of the cannon barrel - there's a reason why they're so long!), even a simple transfer of momentum by a single impact (e.g one Newtonian ball hitting another) isn't instant.

Answer 4

In classical mechanics immediately means "immediately", : all the energy transferred at t=0. (I should qualify this as the chosen answer demonstrates, since really t=0 cannot be reached but only approached as a limit, which can be infinitesimally small). A time lag from the firing to the transfer of all the forward momentum of the explosion will only depend on the time distribution of the whole explosive catching fire. This is statistical mechanics and depends on the density, type etc of the material that is being fired.

Explosive materials may be categorized by the speed at which they expand. Materials that detonate (the front of the chemical reaction moves faster through the material than the speed of sound) are said to be "high explosives" and materials that deflagrate are said to be "low explosives". Explosives may also be categorized by their sensitivity. Sensitive materials that can be initiated by a relatively small amount of heat or pressure are primary explosives and materials that are relatively insensitive are secondary or tertiary explosives.

...

detonation

This term is used to describe an explosive phenomenon whereby the decomposition is propagated by an explosive shock wave traversing the explosive material at speeds greater than the speed of sound (340 m/s). The shock front is capable of passing through the high explosive material at supersonic speeds, typically thousands of metres per second.

So there will be a small time lag before the projectile gets the whole front.

If one starts thinking of the quantum mechanical processes that generate the explosion there is an absolute lower limit to the time interval , given by the Heisenberg uncertainty principle in the form of $\Delta(E)\Delta(t)>\hbar/2$. This is in contrast to the classical case. The HUP is fulfilled within the constraints of the classical explosion energy transfers.

Answer 5

If we want a quick solution to a) how far the ball went, b) what's its exit velocity from the cannon, etc. then we can assume that the ball left the cannon at 100 m/s. Its velocity's x-component can be assumed to be constant, with only the y-component changing due to gravity (e.g., the $v_y = 0$ at the top of the ball's trajectory, but is greater than zero otherwise).

However, if we want to be more picky and realistic, then no the ball does not go from 0 m/s to 100 m/s in 0 s. It may get there quickly, but we must obey ideas such as inertia and impulse. For example, the impulse equation can be written as $F \Delta t = m \Delta v$. If the change in time is zero, then we can't have any change in velocity (meaning going from 0 velocity to some non-zero velocity).

Answer 6

It is certainly true that the acceleration is not instantaneous and occurs over a period of time, as already covered by a number of other answers.

One interesting result of this gradual acceleration that occurs within the barrel that can be observed is that increasing the barrel length results in an increase in the muzzle velocity of the projectile.

For example, this chart of muzzle velocity versus barrel length describes the issue clearly. The bullet is being constantly accelerated by the expanding gases from the deflagrating propellant, and therefore increasing the barrel length (and therefore increasing the time of acceleration) results in a higher muzzle velocity experienced by the bullet.

Answer 7

No object can start moving immediately with velocity $v_0$ at the time $t_0$ when force was applied, because in such case object would have acceleration: $$ \lim_{\Delta t \to 0} \frac {v_0}{(t_0+\Delta t)-t_0} = \frac {v_0}{0} = \infty \tag 1$$

which will tend to infinity. For such acceleration you need, an infinite force, as per $$ F=ma=m\cdot \infty = \infty, \tag 2 $$ for any finite mass greater than zero. Oh, and for infite mass, because $\infty\cdot \infty = \infty$.

Having infinite force is prohibited in Physics. And overall having any infinite quantity is also prohibited.

Unless it's an infinitely small quantity approximated to zero, because $0= \lim_{n \to \infty} \frac 1n$. But we have issues with these things too, because it's very hard to prove that some quantity is zero too. Maybe your measurement devices aren't sensitive enough, so that you simply haven't reached the required scale of $1/n$ to detect that your quantity is actually not zero ? And also there is a thing such as signal noise, due to environment, limiting physics,- such as uncertainty principle or simply due to device impurities, which spoils the true measurement variable. So Physicists aren't sure about plain zeroes too (unlike mathematicians).

Anyways, because infinite force can't exist in nature, infinite acceleration can't exist too. So, no object can acquire any speed instantly. It takes time. Now how much time it takes,- depends on a group of factors like the mass of an object, force magnitude, resistance forces (drag, etc) which tries to stop an object and similar reasons.

Will you perceive subjectively some movement as an instant action, depends on your (or human in general) audio-visual system which makes neuro-impulse responses to the brain from the outer events. If your system response time is greater than a timescale on which the event is happening,- then you will perceive it as an "instant" event. Though it has nothing to do with "instant", but rather with a lag in your response system.