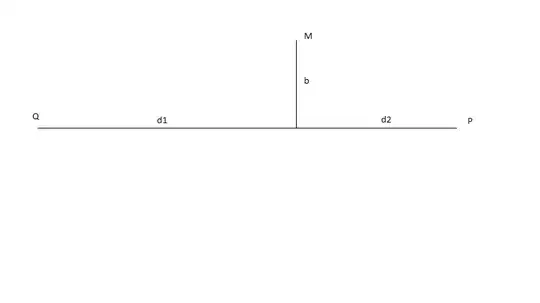
In Einstein's theory of gravity, an electromagnetic wave passing near a massive object is bent from its rectilinear path. We may regard this bending equivalently as due to a medium of refractive index $$\mu_g = 1 - \frac{2\phi}{c^2}$$
where $\phi$ is the gravitational potential due to an object of mass $M$.Consider radiation for a Quasar Q (treated as point like object) reaching observer P as shown in figure. Here $b$ is the distance of closes approach to gravitational object $M$. Show that the optical path length for path QP is given by $$d = d_1 + d_2 + \frac{2MG}{c^2}\left(\ln\frac{4 d_1 d_2}{b^2}\right)$$
- What does "we may regard this bending equivalently as due to a medium of refractive index" mean? If we can treat it as a medium, them what do we take the angle of incidence, refraction, the medium interface etc to be?
- By optical path length of path QP, should we find $\int n(s)ds$ over the line segment QP or should we do it over the actual path taken by light to move from Q to P? And how do we show the last part?