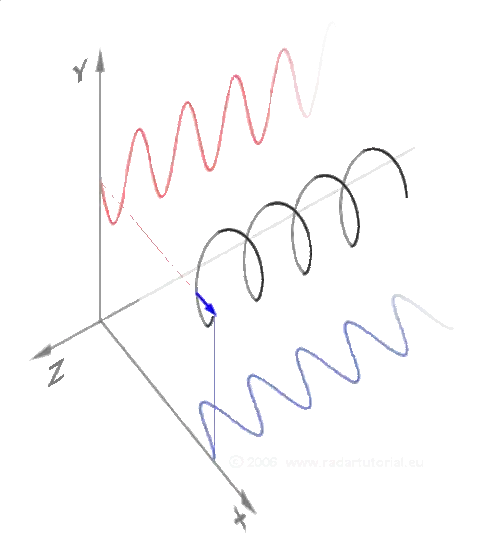
The fact that the period of the gravity train that passes through the center of the Earth is equal to the period of an orbit that skims the Earth's surface is not a coincidence. Consider a polar orbit around Earth (i.e., one that passes directly over the coordinate north and south poles). Now, consider only the north-south motion of the satellite by projecting the motion onto a line parallel with the Earth's axis. What kind of motion is this? Circular orbits have a constant speed, so the 1-D motion must be sinusoidal. The gravity train is just a circular orbit where the motion off the Earth's axis is restricted. Perpendicular forces and motions can be treated independently. See the animation below to illustrate. The spinning arrow shows the path of a satellite, while the straight lines show the path of the gravity train for perpendicular tracks.
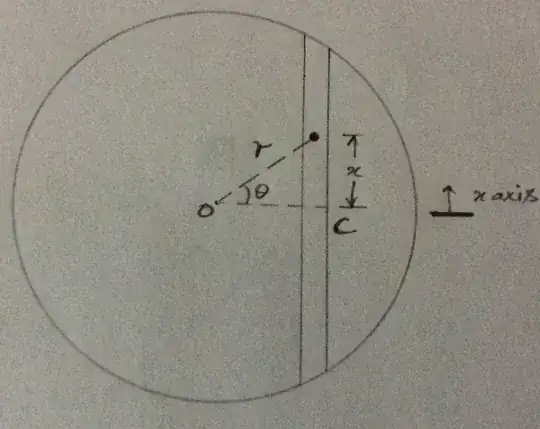
Now, what about gravity trains that don't pass through the Earth's center? First, notice that your expression for the acceleration of the train does not depend on the distance from the Earth's center. As long as the track is symmetric about the Earth's radius, then you will get the same train motion no matter the depth of the track. The ends of the track do not have to connect to the surface. You can also reason that the depth of the gravity train track does not matter by starting with a track that connects to the surface at both ends and then adding a shell around the entire planet to increase its radius. Inside a spherical shell, the gravitational force is zero, so burying the track does nothing to the motion.
To start to demonstrate this, let's prove a similar fact about circular orbits: the period of an orbit that skims a planet's surface depends only on the planet's density, not its size.
$$F = m\frac{v^2}{R} = \frac{GMm}{R^2}$$
where $F$ is the gravitational force, $m$ is the mass of the satellite, $M$ is the mass of the planet, $v$ is the speed of the orbit, $R$ is the radius of the planet, and $G$ is the gravitational constant.
$$v^2 = \frac{GM}{R}$$
$$\left(\frac{2\pi{}R}{T}\right)^2 = \frac{GM}{R}$$
where $T$ is the period of the orbit.
$$T = \sqrt{\frac{4\pi{}^2R^3}{GM}}$$
$$T = \sqrt{\frac{4\pi{}^2R^3}{G\rho\frac{4}{3}\pi{}R^3}}$$
$$T = \sqrt{\frac{3\pi}{G\rho}}$$
where $\rho$ is the density of the planet.
Now, starting from your expression for the train acceleration:
$$a = -\frac{4}{3}\pi\rho{}Gd$$
we can derive an equivalent mass-spring system(*) with a spring constant $k$ given by
$$k = \frac{F}{d} = \frac{ma}{d} = \frac{4}{3}\rho{}Gm.$$
The period of this mass-spring system, and thus of the train, is
$$T = 2\pi\sqrt{\frac{m}{k}} = \sqrt{\frac{4\pi^2m}{\frac{4}{3}\pi\rho{}G}} = \sqrt{\frac{3\pi}{\rho{}G}}$$
Notice that this is the same period as the satellite.
TL;DR: The gravity train is a 1D projection of the 2D circular orbit where the length of the train track is the same as the diameter of the orbit. The time to traverse the track is the same no matter the length or the depth because the period of a surface-skimming orbit around a constant-density planet is independent of the size of the planet.
(*) Everything is physics is ultimately a mass on a spring.