-1

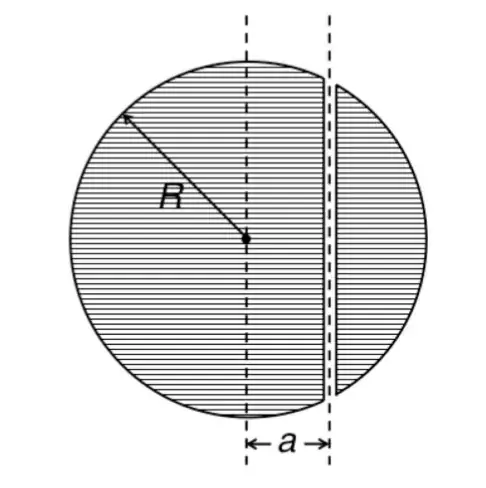
There is a planet with a straight tunnel through it which does not pass trough the center.

enter image description here

I want to solve how a mass will move in that tunnel.

This is what i have done

By Gauss' law, the gravity for some $r<R$ is $\mathbf g(r) = -k r\mathbf{\hat r} $, where $k$ is a constant.

By Newton's second law,

$\begin{align} m\ddot r &= mg\\ &=-mkr \\ \Rightarrow & \ddot r + kr=0 \end{align}$

Since the tunnel does not pass though the center, $r$ satisfies that $r\cos\phi=a$. Where $\phi$ is the angle measured from $x$-axis (the origin is in the center of the planet).

Using chain rule, $\ddot r$ can be written as \begin{align} \ddot r = \dfrac{d}{dt}\dfrac{dr}{dt}= \dfrac{d}{dt}\left( \dfrac{dr}{d\phi} \dfrac{d\phi}{dt}\right)= \dfrac{dr}{d\phi} \dfrac{d^2\phi}{dt^2}=r'\ddot\phi \end{align}

Then, taking the derivative of $r$ with respect to $\phi$ and substituting into the equation of motion gives,

\begin{align} r'\ddot\phi+kr&=a\ddot\phi \sec\phi \tan\phi + ka\sec\phi=0 \\ \Rightarrow & \ddot\phi\tan\phi+k=0 \\ \Rightarrow & \ddot\phi+k\cot\phi=0 \end{align}

My question

I ask for if my condition for $r$ ($r\cos\phi=a$) is correct, or there is something that i missing. Does not the differential equation for $\phi$ must lineal or similar to an harmonic oscillator eq?

In the case in which my equations are right. How to solve that kind of eqs.?

Any suggestion will be helpful.

Gabriel Sandoval
  • 454

2 Answers2

0

This problem is identical to the so-called gravity train problem.

It can be shown quite easily that the object, travelling without friction through the tunnel, will behave like a harmonic oscillator (full derivation).

With $\theta$ the angle between the tunnel and the line connecting the one end of the tunnel and the centre of the planet, $R$ the planet's radius, $g$ its gravitational acceleration, then the distance travelled is:

$$r(t)=R\cos\theta \cos\sqrt\frac{g}{R} t$$

So the angular frequency $\omega$ is:

$$\omega=\sqrt\frac{g}{R}$$

Interestingly, it can also be shown that:

$$\frac{g}{R}=G\rho \frac43 \pi$$

So the travel time between two equally opposite points does not depend on the radius, provided the density is the same.

Gert
  • 35,561
0

There are two errors in your derivation as it stands:

  1. If we express Newton's Law $\vec{F} = m \vec{a}$ in terms of polar coordinates $r$ and $\phi$, it is not true that $F_r = m \ddot{r}$ (as you assume in your first step. Rather, we have $$ \vec{a} = (\ddot{r} - r \dot{\phi}^2) \hat{r} + (r \ddot{\phi}^2 + 2 \dot{r} \dot{\phi}) \hat{\theta}, $$ (See Wikipedia for a derivation.) This means that your equation $m \ddot{r} = F_r$ is incorrect as it stands, unless you know that $\dot{\phi} = 0$ some reason.

  2. In addition to the force of gravity, there will also be a constraint force from the walls of the tunnel or the track that the car is sliding on or what-have-you. After all, if there wasn't a second force of this sort acting on the car, then it would accelerate directly towards the center of the Earth when released from rest, not along the path of the tunnel. This means that both of your equations of motion are wrong, unless you can argue that the force from the tunnel walls vanishes.

There is one special case where the force from the tunnel vanishes and $\dot{\phi} = 0$: when the tunnel passes directly through the center of the Earth. In this case, $\phi$ will be a constant from symmetry, and no force will be necessary from the track/walls to keep the car in the tunnel. In this limited case, your equations are correct; but for the off-center tunnel in your problem, you have to be cleverer than that.

Michael Seifert
  • 54,357