Here is a question from my book.
I need to know which force is acting on the ball, making it move outwards?
It cannot be centrifugal force, as centrifugal force acts if the particle is moving in a circle. Here it is clearly not. Moreover centrifugal force acts when it is seen from the point of view of the ball itself (pseudo forces act only in an accelerated frame). What if I look at it from the ground? Which force will then be responsible for making it move outwards?
Here is an attempt to explain what is going on in the (inertial) frame of reference of the world:
The red vector is the force from the side of the groove on the ball: as a result the ball starts to move. Initially, it will get the same lateral speed as the groove - if it's at a distance $r$, and the disk rotates at $\omega$, the velocity will be $v=r~\omega$.
A moment later, the groove will be at a different angle - but the ball tries to keep going in a straight line. It will have moved to a new radial direction, where the groove is going faster than the ball. As a result, it will once again feel a force of the wall, and it will accelerate in a new direction; I tried to indicate the new velocity as the vector sum of the old velocity plus the acceleration.
Obviously you can repeat the diagram for subsequent positions of the disk.
In the rotating frame of reference of the disk, you can describe the same thing in a different way. In a rotating frame of reference, there appear to be two fictitious forces: the centrifugal force that makes the object "want to move away from the center", and the Coriolis force that is only apparent if the object has a velocity in the rotating frame of reference.
When the ball is stationary in the groove (in the rotating frame of reference), the only force it experiences is the centrifugal force (this is right after the initial impulse that will have given the ball the same velocity as the part of the groove where it was placed). As soon as it starts moving outwards (under the influence of the centrifugal force) it will also start to swerve (under the influence of the Coriolis force). The groove will exert a force equal and opposite to the Coriolis force to keep the ball moving in a straight line in the groove.
In the rotating frame of reference, the radial acceleration of the ball can be calculated directly from the centrifugal force. The total velocity can be arrived at by calculating both the radial and tangential components of the velocity (tangential velocity is $r\omega$).
I will leave the details up to you.
Technically it's the groove that's exerting a mechanical force on the ball pushing it in the direction the groove is moving in. Inertia is why the ball travels outward because more of it's momentum is in the outward direction as opposed to the inward direction. The groove constantly applying a force and altering the ball's momentum ensures that the majority of it's momentum will always be in the outward direction.
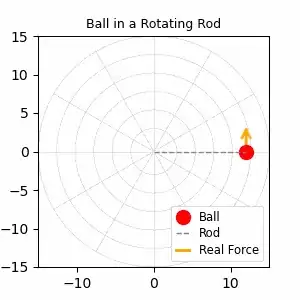
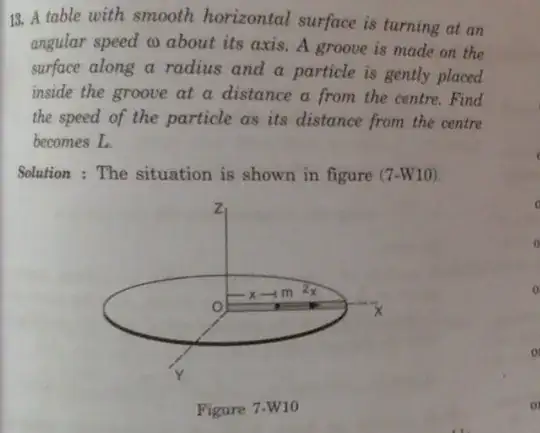
We’ve got the familiar ball-in-a-rotating-rod setup. The rod spins at constant speed $\omega \ rad/s$ and the ball of mass $m$ can slide only along the groove. At $t=0$ you drop the ball at $(r_0,0)$. In inertial coordinates its path is
$$ \gamma(t)= \begin{bmatrix}x(t)\\[4pt]y(t)\end{bmatrix} = r(t) \begin{bmatrix}\cos(\omega t)\\[2pt]\sin(\omega t)\end{bmatrix}, \qquad r(0)=r_0. $$
After two rounds of the product rule you get
$$ \frac{d^2x}{dt^2} =\Bigl(\frac{d^2r}{dt^2}-\omega^2r\Bigr)\cos(\omega t) -2\omega\,\frac{dr}{dt}\,\sin(\omega t), $$
$$ \frac{d^2y}{dt^2} =\Bigl(\frac{d^2r}{dt^2}-\omega^2r\Bigr)\sin(\omega t) +2\omega\,\frac{dr}{dt}\,\cos(\omega t). $$
Bundle those into one tidy vector:
$$ \frac{d^2\gamma}{dt^2} = \Bigl(\frac{d^2r}{dt^2}-\omega^2r\Bigr) \begin{bmatrix}\cos(\omega t)\\[2pt]\sin(\omega t)\end{bmatrix} + 2\omega\,\frac{dr}{dt} \begin{bmatrix}-\sin(\omega t)\\[2pt]\cos(\omega t)\end{bmatrix}. $$
Note: the first vector is radial (along the rod), the second is sideways (perpendicular to the rod). They’re orthogonal—check the dot product.
By Newton’s second law, the total force $F$ acting on the ball satisfies
$$F=m \frac{d^2\gamma}{dt^2}.$$
On the other hand, the only real force acting on the ball is the normal push from the groove (or rod). This force restricts the motion of the ball: it allows free movement along the groove, but responds to any motion perpendicular to the groove with a push perpendicular to the groove, carrying the ball along the rotating track. In particular the force is always perpendicular to the groove. That means the total force $F$ has no component in the direction of the groove. So the radial component of Newton’s second law must vanish. That gives
$$ \Bigl(\frac{d^2r}{dt^2}-\omega^2r\Bigr)=0 \quad\Longrightarrow\quad \frac{d^2r}{dt^2}-\omega^2r=0. $$
The actual push from the groove is therefore
$$ \mathbf F = 2m\omega\,\frac{dr}{dt} \begin{bmatrix}-\sin(\omega t)\\[2pt]\cos(\omega t)\end{bmatrix}. $$
The little ODE we just found is
$$ \frac{d^2r}{dt^2}=\omega^2r. \tag{1} $$
All its solutions look like
$$ r(t)=A\,e^{\omega t}+B\,e^{-\omega t}. \tag{2} $$
If $\omega>0$ the $A$-term blows up, the $B$-term dies out.
The only way you don’t shoot off to infinity is to fine-tune so $A=0$.
For the gentle release you said $r(0)=r_0$ and $\dfrac{dr}{dt}(0)=0$. That forces $A=B=r_0/2$, giving
$$ \gamma(t)=\frac{r_0}{2}\bigl(e^{\omega t}+e^{-\omega t}\bigr) \begin{bmatrix}\cos(\omega t)\\[2pt]\sin(\omega t)\end{bmatrix}. $$
So unless you nailed that special inward kick ($A=0$), the ball’s distance to the origin $r(t)$ grows exponentially and it flies out along the rod.
I made two animations of the setup in the exercise.
In the first clip the radius blows up so fast that the ball flies off the screen almost immediately—pretty dull once it heads toward $\infty$.
In the second clip I let the camera box rescale on the fly, so the ball always stays in view and you can watch the whole spiral.
Keep in mind the two movies run on different time scales, so “one second” in the first is not the same real-time stretch as “one second” in the second.
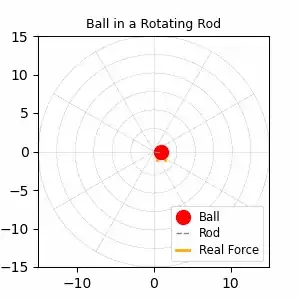
This animation is for the atypical case $A = 0$.
You could think of this in terms of Fictious Forces.
What if i look at it from the ground? Which force will be then responsible to make it move towards the left?
Source: Coriolis Force
In the inertial frame of reference (upper part of the picture), the black ball moves in a straight line. However, the observer (red dot) who is standing in the rotating/non-inertial frame of reference (lower part of the picture) sees the object as following a curved path due to the Coriolis and centrifugal forces present in this frame.
In your example, the groove constrains the ball from moving sideways.
As this a homework type question, I can give you an outline and references for you to read yourself. We have Newton's laws for when we are examing an inertial (non accelerating) frame of reference. When we move to a rotating frame of reference, we acquire extra forces, called either inertial forces or pseudo forces.
These forces are called the Coriolis Force and Centrifugal Force
You can read up more on how these forces work at Rotating Frames of Reference and Forces Involved in Circular Motion
In order for the ball to stay at a constant distance from the center of rotation at a constant angular velocity, the net force on the ball would have to point inwards, from the ball towards the center of rotation (i.e. centripetal force).
However, the only "real" force acting on the ball is the normal force from the side of the groove, which points tangentially. So, the net effect on the ball is that the direction of its velocity vector is constantly being turned to point outward radially.
