Euler Rotations in Ordinary Space

Question

I'm reading LittleJohn's notes on Rotations in Ordinary Space on Quantum Mechanics. Link: http://bohr.physics.berkeley.edu/classes/221/1011/notes/classrot.pdf. I'm trying the last question given in the document one the last page:

It is claimed that every proper rotation can be written in Euler angle form. Find the Euler angles $(\alpha, \beta, \gamma)$ for the rotation $R(\hat{x}, π/2)$.

The formula for the Euler Rotation being used is given by $(58)$ in the notes.

My question is: is there a systematic way to figure out the Euler Angles, via the use of some formula, for relatively easy rotations like this? Or would have to figure out how the basis vectors transform under the said rotation and then try and figure out the Euler Angles by inspection or solving a system of equations by representing the sequence of Euler rotations in matrix form (if that's possible)?

Also, how does one go about solving this problem for rotations about an arbitrary axis? Is that a very difficult problem?

Answer 1

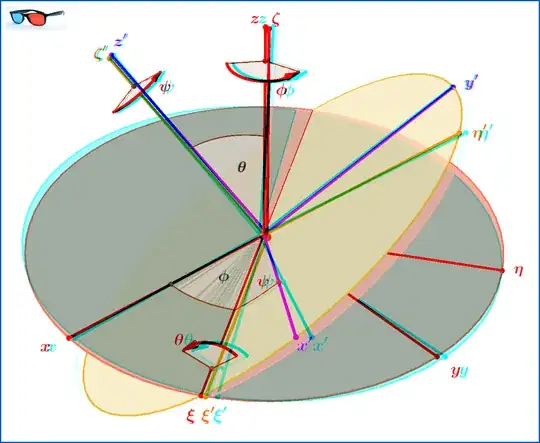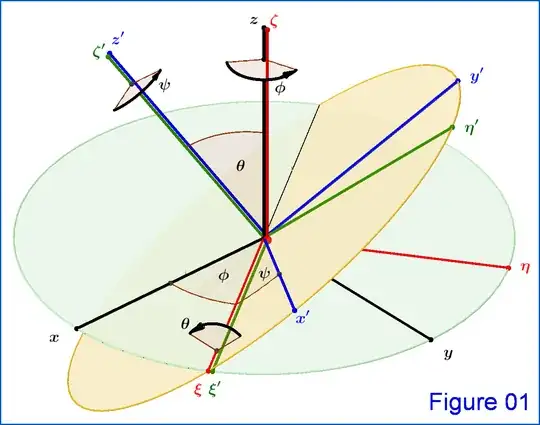
A rotation of coordinate axes is represented via the Euler angles $\:\psi,\theta,\phi \:$ by the matrix,see Figure 01⁽¹⁾. ^{\begin{equation} \mathrm{A}\left(\psi,\theta,\phi\right)= \begin{bmatrix} \cos\psi \cos\phi - \cos\theta \sin\phi \sin\psi & \cos\psi \sin\phi + \cos\theta \cos\phi \sin\psi & \sin\psi \sin\theta \\ -\sin\psi \cos\phi - \cos\theta \sin\phi \cos\psi & -\sin\psi \sin\phi + \cos\theta \cos\phi \cos\psi & \cos\psi \sin\theta \\ \sin\theta \sin\phi & -\sin\theta \cos\phi & \cos\theta \end{bmatrix} \tag{01} \end{equation}} according to the following scheme

\begin{equation} xyz \quad \Longrightarrow \quad \xi \eta \zeta \quad \Longrightarrow \quad \xi' \eta' \zeta' \quad \Longrightarrow \quad x'y'z' \tag{02} \end{equation}

The 1st rotation $\mathrm{D}$ is around axis $z$ by angle $\phi$, so $\zeta \equiv z$. The 2nd rotation $\mathrm{C}$ is around axis $\xi$ (the "new $x$-axis") by angle $\theta$, so $\xi' \equiv \xi$. The 3rd rotation $\mathrm{B}$ is around axis $\zeta'$ by angle $\psi$, so $z' \equiv \zeta'$.

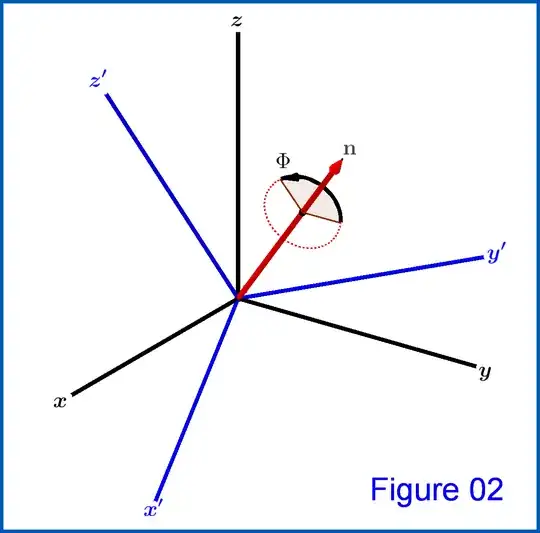
Also, another representation is via the angle of rotation $\:\Phi \:$ around a direction $\:\mathbf{n}=(n_1,n_2,n_3)\:$, where $\:\mathbf{n}\:$ a unit vector and $\:n_1,n_2,n_3\:$ its $\:x,y,z\:$ components respectively, see Figure 02⁽²⁾

^{\begin{equation} \mathrm{A}\left(\mathbf{n},\Phi\right)= \begin{bmatrix} \cos\Phi+(1-\cos\Phi)n_1^2 & (1-\cos\Phi)n_1n_2+\sin\Phi n_3 & (1-\cos\Phi)n_1n_3-\sin\Phi n_2\\ (1-\cos\Phi)n_2n_1-\sin\Phi n_3 & \cos\Phi+(1-\cos\Phi)n_2^2 &(1-\cos\Phi)n_2n_3+\sin\Phi n_1\\ (1-\cos\Phi)n_3n_1+\sin\Phi n_2 & (1-\cos\Phi)n_3n_2-\sin\Phi n_1 & \cos\Phi+(1-\cos\Phi)n_3^2 \end{bmatrix} \tag{03} \end{equation}}

---

^{(1) "Classical Mechanics" , H.Goldstein-C.Poole-J.Safko, 3rd Edition. Figure 01 is a redrawing of FIGURE 4.46 therein. The matrix $\:\mathrm{A}\left(\psi,\theta,\phi\right)\:$, see equation (01) above, is equation 4.46 therein. This matrix is the product \begin{equation} \mathrm{A}=\mathrm{B}\mathrm{C}\mathrm{D} \tag{foot-01} \end{equation} where \begin{equation} \mathrm{D}= \begin{bmatrix} \cos\phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \mathrm{C}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & \sin\theta \\ 0 & - \sin\theta & \cos\theta \end{bmatrix}, \quad \mathrm{B}= \begin{bmatrix} \cos\psi & \sin\psi & 0 \\ -\sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{foot-02} \end{equation} as in equations (4.43), (4.44) and (4.45) therein.}

^{(2) For the expression (03) of $\:\mathrm{A}\left(\mathbf{n},\Phi\right)\:$ use equation (08) replacing $\:\theta\:$ by $\:-\Phi\:$ in my answer in -Rotation of a vector-}

^{(3) I suggest to read the David Hammen's answer here -Euler angles derivation-}

Answer 2

As an answer to the last part of your question, let us derive the 3x3 matrix for rotating an object (eg: a 3-vector) by $s$ radians about an arbitrary direction specified by the unit vector $\hat{n}$. This means put your right hand thumb along the unit vector $\hat{n}$ and rotate the object by pushing with your right hand fingers through the angle $s$. For me, this is a much easier way to parameterize and visualize an arbitrary rotation than Euler angles. Define three angles $(\theta_1,\theta_2,\theta_3)=s \ \hat{n}$. Notice $s=\sqrt{\theta_1^2+\theta_2^2+\theta_3^2}$. $$ \Theta = \begin{bmatrix} 0 & -\theta_3 & \theta_2 \\ \theta_3 & 0 & -\theta_1 \\ -\theta_2 & \theta_1 & 0 \\ \end{bmatrix} $$ First, suppose all the rotation angles are very small (ie: <<1) which we do by dividing the $\theta$ by a big $N$. Then consider rotating a vector in the plane perpendicular to each of the three axis, for example the small angle $\Delta\theta_3=\frac{\theta_3}{N}$ about the 3-axis for a vector in the 1-2 plane. By drawing pictures and thinking you will conclude that for these small rotations $$ M(\frac{\Theta}{N})=I+\frac{\Theta}{N} $$ Now multiply N of these small rotations together in order to get the full rotation by $\Theta$. In the limit of large N this is equal to $e^{\Theta}$ by a mathematical identity. $$ M(\Theta)=\lim_{N\to\infty} (I+\frac{\Theta}{N})^N=e^{\Theta} $$ Finally we expand $e^{\Theta}$ in a power series and matrix multiply $\Theta$ 's together to calculate each term. You will find $\Theta^3=-s^2\Theta$. $$ \begin{align} M(\Theta) & =e^{\Theta} \\ & =I+\Theta+\dfrac{\Theta^2}{2!}+ \dfrac{\Theta^3}{3!}+ \dfrac{\Theta^4}{4!} +… \\ & =I+\Theta(1-\frac{s^2}{3!}+\frac{s^4}{5!}-...)+\Theta^2(\frac{1}{2!}-\frac{s^2}{4!}+\frac{s^4}{6!}-...) \\ \\ M(\Theta) & =I+ \frac{\Theta}{s}sin(s)+\frac{\Theta^2}{s^2}(1-cos(s)) \end{align} $$ This $M(\Theta)$ is the matrix for rotating about an arbitrary vector $\vec{A}$ by angle $s$. As an example, suppose $\vec{A}=(0,0,\theta)$, which is a rotation about the z-axis by theta. Then $s=\theta$ and the final equation for M yields the familiar rotation matrix $$ M(\Theta) = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$