Why correlation length diverges at critical point?

Question

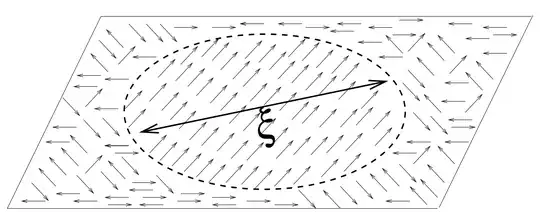
I want to ask about the behavior near critical point. Let me take an example of ferromagnet. At $T < T_c$, all spins are aligned to the same direction thus it is in the ordered state, scale invariant, its correlation length is effectively infinite. At $T > T_c$, all spins are aligned randomly so it is disordered state. However, in my understanding, we say the system is scale invariant and its correlation length diverges only at critical point.

What is wrong in my understanding? Furthermore, could you explain an intuitive region why at critical point, the correlation length should diverge?

Answer 1

It is not the correlation length of the system that you should look at, but the correlation of the fluctuations. If T>>Tc the spins are randomly oriented and the lenghtscale of fluctuations is very small. As you get closer to Tc, the fluctuations become more correlated, and lenghtscale increases toward infinity. Similarly for the ferromagnet at temperatures much less than Tc, all spins are aligned. The fluctuations at 0 < T << Tc have short correlation lengths. As you heat the system, it is still mostly ordered, but the number of spins pointing in the opposite direction increases, and so does the correlation length of these fluctuations

Answer 2

I think your trouble is that a correlation length $\xi$ is not to be interpreted as correlation in the sense of statistics, e.g.

$ \frac{\langle(s(x)-\langle s(x) \rangle)(s(y)-\langle s(y)\rangle)\rangle}{\sqrt{\langle\left( s(x)-\langle s(x)\rangle\right)^2 \langle(s(y)-\langle s(y)\rangle)^2 \rangle)}}$,

but rather defined via $ \langle(s(x)-\langle s(x)\rangle)(s(y)-\langle s(y)\rangle)\rangle=e^{-|x-y|/\xi}$

(see for example https://physics.stackexchange.com/q/59690).

Assume that, at zero temperature, all spins are "frozen" and perfectly aligned and hence perfectly correlated (in the statistical sense). However, since $s(x)=\langle s(x) \rangle$ and $s(y)=\langle s(y) \rangle$ in this case, it follows that $\xi=0$.

As far as the second part of the question is concerned: Critical points are phase transitions that correspond to fixed points in the renormalization group flow. What this means is that the process of consecutively dividing the spin lattice into blocks, integrating them out and constructing a new Hamiltonian between those blocks has reached a fixed point: The form of the Hamiltonian does not change any longer, only its parameters (couplings) get re-adjusted with any further block-spin operation. This in turn means that the system has lost its scale and has become scale-free. So if I were to take two pictures of the material, one of size one inch and the other one of size one micro-inch, you could not tell me which one is which. The only way to describe this mathematically is by assuming a power-law which yields $\xi(T) \sim (T-T_c)^{-\nu}$ where $T_c$ is the critical temperature and $\nu$ is the scaling dimension that is not necessarily integer. Hence the correlation length diverges at the critical point.

Answer 3

Since technical derivation and explanation of correlation length have already been discussed in detail, I would rather share my understanding of this subject matter.

The notion of correlation length is quite general in the study of thermal or quantum phase transition. It is the only relevant length scale near the critical point.

Let's think about a magnetic system. Usually, nearby spins tend to be correlated. Away from the critical point, $T \neq T_c$, their correlation extends to a certain distance $\xi$, called the correlation length. This is the typical size of the regions in which the spins assume the same value, as shown below

Where the correlation length gives the size of the magnetic domain. Of course, one can make its definition more precise in terms of the asymptotic behavior of the correlation function, but the physical picture remains the same as corresponds to the diagram above.

At the critical point, the system becomes scale invariant. Therefore, no matter in which direction we look and how far we look, the system appears to be the same. Which indeed means that the correlation becomes infinite.