Electronic transitions and fluorescent states are very short, phosphorescence can be fairly short or many hours long (like glow sticks). An electronic transition, where a photon passes on its energy, occurs rapidly, as does the vibrational relaxation or internal conversion which occurs in about a picosecond or less. Fluorescence lifetimes are typically four orders of magnitude slower than vibrational relaxation, giving the molecules sufficient time to achieve a thermally equilibrated lowest-energy excited state prior to fluorescence emission.
"Phosphorescence decay is similar to fluorescence, except the electron undergoes a spin conversion into a "forbidden" triplet state (T(1)) instead of the lowest singlet excited state, a process known as intersystem crossing. Emission from the triplet state occurs with lower energy relative to fluorescence, hence emitted photons have longer wavelengths. With delayed fluorescence, the electron first decays into the triplet state, and then crosses back over into the lowest singlet excited state before returning to the ground state.".
Source/proof:
Why for electronic transitions dephasing is much faster than radiative emission?
Wikipedia's webpage "Franck–Condon Principle" explains:
"Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level to another will be more likely to happen if the two vibrational wave functions overlap more significantly.".
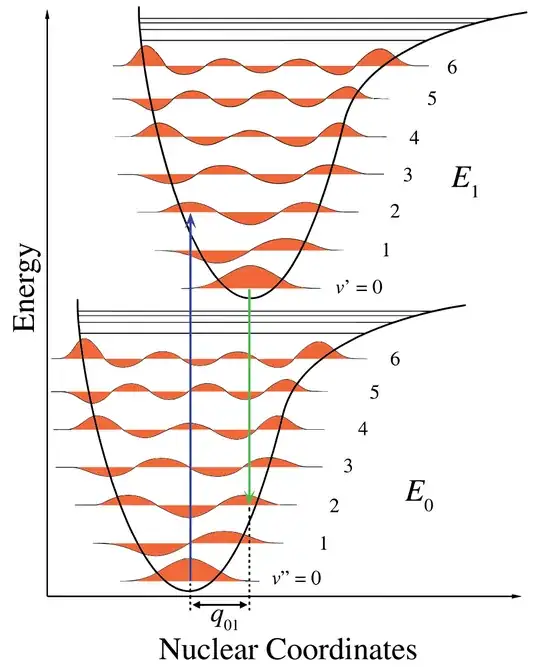
$\scriptsize\text{Figure 1. Franck–Condon principle energy diagram. Since electronic transitions are very fast compared with nuclear motions,}$
$\scriptsize\text{vibrational levels are favored when they correspond to a minimal change in the nuclear coordinates. The potential wells are}$
$\scriptsize\text{shown favoring transitions between v = 0 and v = 2.}$
"In the quantum mechanical picture, the vibrational levels and vibrational wavefunctions are those of quantum harmonic oscillators, or of more complex approximations to the potential energy of molecules, such as the Morse potential. Figure 1 illustrates the Franck–Condon principle for vibronic transitions in a molecule with Morse-like potential energy functions in both the ground and excited electronic states. In the low temperature approximation, the molecule starts out in the v = 0 vibrational level of the ground electronic state and upon absorbing a photon of the necessary energy, makes a transition to the excited electronic state. The electron configuration of the new state may result in a shift of the equilibrium position of the nuclei constituting the molecule. In the figure this shift in nuclear coordinates between the ground and the first excited state is labeled as q$_{01}$. In the simplest case of a diatomic molecule the nuclear coordinates axis refers to the internuclear separation. The vibronic transition is indicated by a vertical arrow due to the assumption of constant nuclear coordinates during the transition. The probability that the molecule can end up in any particular vibrational level is proportional to the square of the (vertical) overlap of the vibrational wavefunctions of the original and final state (see Quantum mechanical formulation section below).".
Further down the webpage "Franck–Condon Principle", in section "Quantum Mechanical Formulation" it explains:
The table of Napierian extinction coefficients below gives the range of extinction coefficients for the possible combinations of allowed and forbidden spin and orbital selection rules:
$$\qquad\qquad \mathbf{\text{Intensities of electronic transitions}} \\
\begin{array}{c|c}
& \text{Range of extinction coefficient (ε) values (mol}^{−1} \text{cm}^{−1}\text{)} \\
\hline \\
\text{Spin and orbitally allowed} & \text{10}^3 \,\text{to}\, 10^5 \\
\text{Spin allowed but orbitally forbidden} & 10^0 \,\text{to}\, 10^3 \\
\text{Spin forbidden but orbitally allowed} & 10^{−5} \,\text{to}\, 10^0 \\
\end{array}
$$
Why for vibrational transitions non-radiative relaxations are faster than radiative ones?
This short webpage: "Jablonski Diagram" from Sam Houston State University has this easy explanation:
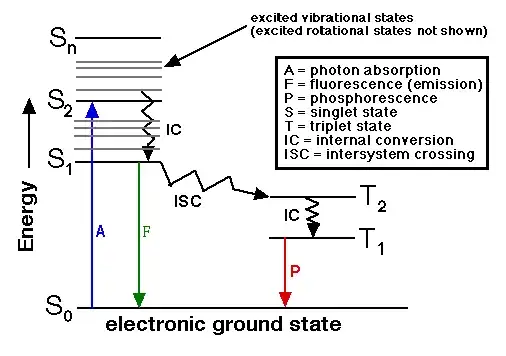
"Once a molecule has absorbed energy in the form of electromagnetic radiation, the $\color{blue}{\text{blue}}$ line, there are a number of routes by which it can return to ground state.
If the photon emission (shown here as a short wavelength, that is downward pointing, "long" $\color{green}{\text{green}}$ line in the diagram) occurs between states of the same spin state (e.g. S$_1 \rightarrow$ S$_0$) this is termed fluorescence. If the spin state of the initial and final energy levels are different (e.g. T$_1 \rightarrow$ S$_0$), the emission (loss of energy) is called phosphorescence. In the diagram this is depicted by a longer wavelength (lower energy) and therefore shorter length $\color{red}{\text{red}}$ line.
Since fluorescence is statistically much more likely than phosphorescence for most molecules, the lifetimes of fluorescent states are very short (1 x 10$^{-5}$ to 10$^{-8}$ seconds) and phosphorescence somewhat longer (1 x 10$^{-4}$ seconds to minutes or even hours; think about glow-in-the-dark flying disks).
Three nonradiative deactivation processes are also significant here: internal conversion (IC), intersystem crossing (ISC) and vibrational relaxation. Examples of the first two can be seen in the diagram. Internal conversion is the radiationless transition between energy states of the same spin state (compare with fluorescence-a radiative process). Intersystem crossing is a radiationless transition between different spin states (compare to phosphorescence).
Vibrational relaxation, the most common of the three - for most molecules, occurs very quickly ($\lt\,$ 1 x 10$^{-12}$ seconds) and is enhanced by physical contact of an excited molecule with other particles with which energy, in the form of vibrations and rotations, can be transferred through collisions. This means that most excited state molecules never emit any energy because in liquid samples the solvent, or in gas phase samples, other gas phase molecules that are present "steal" the energy before other deactivation processes can occur.".

