1

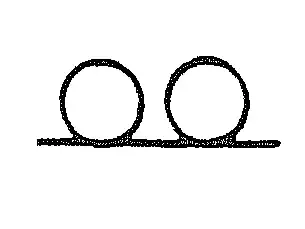
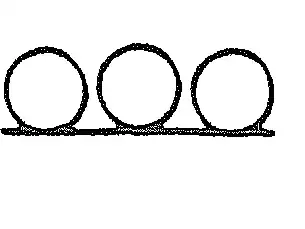I will refomulate my question(Geometric series for two-point function) because it seems that i did not make it clear. In order to have

$G_c^{(2)}(x_1,x_2)=G_0^{(2)}+G_0^{(2)}\Pi G_0^{(2)}+G_0^{(2)}\Pi G_0^{(2)}\Pi G_0^{(2)}+...$

the reducible diagram must be of some form. for example the 2 loop in $\phi$ theory is of the form

png

and the 3 loop is

png

how can we prove that there is not multiplicative constant say for example a 7 times the 2 loop and a 8 times the 3 loop that would invalidate the geometrical series?

Community
  • 1
Paul Dirac
  • 11

1 Answers1

0

One way to find out what the symmetry factors (or whatever other factors) are with which different diagrams should be multiplied is to expand the Feynman path integral. One would add source terms for all the fields in the Lagrangian. Then one can pull all the interaction terms out of the path integral by replacing the fields in these terms with functional derivatives with respect to the sources. What remains inside the integrals are only the kinetic terms. These can be integrated out by completing the squares, so that only the propagators, connected with sources, remain. The latter now serve as generating functions on which the exponential function containing the interaction terms act. One can expand these exponential functions and then let the individual terms act on the generating function containing the propagators. In this way one would obtain all the possible Feynman diagrams together with the correct numerical (symmetry) factors.

flippiefanus
  • 16,824