What is the smallest number of photons needed to make a "light wave"? In other words, how many (coherent?) photons start to exhibit classical behavior?
For example, how many photons are needed to get linear polarization? (Single photon has circular polarization.)
Even though there is a single photon in a volume of your choice the light is still a wave.
An experiment was performed which proved this. In this experiment a Michelson interferometer was set up and the incident light is so weak that only one photon was in the whole setup at a time. A photographic plate was used to detect the interference pattern. Now just imagine one photon is being split up by the beam splitter and combined on the detector to give the interference pattern.
After several hours of the exposure people have recovered the classical interference pattern is generated (as if one photon has interfered with itself).
Hence the interference pattern (the classical proof that light is a wave) is just our perception, It remain wave all the time whether it is one photon or one million.
Correction, a single photon does not have a circular polarization. It has spin +1 or -1 to the direction of its motion.
Left and right handed circular polarization, and their associate angular momenta.
The way the classical wave emerges from the quantum mechanical level of photons is given in this blog entry, and it needs quantum field theory to understand it. In a summary, the wave function of a photon is controlled by a quantized maxwell equation, and the complex wavefunction has the information and phases necessary to build up the classical electric and magnetic field of the classical electromagnetic wave.
The number of photons for a given frequency of light can be estimated by dividing the classical power by the energy of each individual photon. An order of magnitude estimate of when the classical behavior appears can be seen in this double slit experiment
single-photon camera recording of photons from a double slit illuminated by very weak laser light. Left to right: single frame, superposition of 200, 1’000, and 500’000 frames.
Single photons below 200 in number look practically random on the photo One sees that already with 1000 photons the interference of the classical type is evident.
This also demonstrates the probabilistic nature of the photon's spatial behavior, as the classical interference pattern measures the probability of finding a photon at (x,y). At the same time, the macroscopic, point nature of a single photon , a dot on the ccd , is evident.
Let us look at coherent states $$ |\alpha\rangle~=~e^{-|\alpha|^2/2}e^{\alpha a^\dagger}|0\rangle $$ $$ e^{-|\alpha|^2/2}\sum_{n=0}^\infty \frac{(\alpha)^n (a^\dagger)^n}{n!}|0\rangle $$ If you have a classical system it means overlap between states is small. We then look at over lap $\langle\alpha'|\alpha\rangle$ $$ \langle\alpha'|\alpha\rangle~=~e^{-(|\alpha|^2~+~|\alpha'|^2)/2}\sum_{m,n=0}^\infty \langle 0|\frac{(\alpha)^m a^m}{m!}\frac{(\alpha'^*)^n (a^\dagger)^n}{n!}|0\rangle $$ $$ =~e^{-(|\alpha|^2~+~|\alpha'|^2)/2}\sum_{m,n=0}^\infty\frac{(\alpha)^m}{m!}\frac{(\alpha'^*)^n }{n!}\langle m|n\rangle~=~e^{-(|\alpha|^2~+~|\alpha'|^2)/2}\sum_{n=0}^\infty\frac{(\alpha)^n(\alpha')^n}{n!^2}. $$ The key factor to look at is $e^{-(|\alpha|^2~+~|\alpha'|^2)/2}$ and what when does this go to zero. Below is a diagram of the meaning of $\alpha$.
For the value of large momentum this factor $e^{-(|\alpha|^2~+~|\alpha'|^2)/2}$ is small.
There is no hard boundary between the quantum and classical worlds. However, let us consider light with a wavelength $\lambda~=~400nm$ which is near the middle of the optical range. The energy of a photon is $E~=~7.8\times 10^{-20}$j. Let us consider a $1000$ watt light source, which is comparable to direct sunlight. This light is about $1.3\times 10^{22}$ photons per second. Then in one second this amounts to that many photon and the momentum $p~=~E/c$ is then $3\times 10^{-6}kgm/s$. The momentum of each photon is about $2.5\times 10^{-28}$kgm/s. Now consider expanding the momentum in this diagram by that expansion and consider that this factor $e^{-(|\alpha|^2~+~|\alpha'|^2)/2}~\sim~e^{-10^{-28}}$ which is pretty small! This pretty clearly puts it is a classical domain.
Light never completely behaves as a particle. Light never completely behaves as a wave. As pointed out by hsinghal, the Michelson interferometer showed that, even at the "single photon" level, we still see wave behaviors. These behaviors are well modeled by quantum mechanics, which treats light as neither a pure wave nor a pure particle.
As you "add photons" the "light is a wave" approximation gives you better and better results. However, as for "how many photons are needed to make a light wave," the answer depends on just how good you want that light wave model to approximate the behavior you see. This answer is entirely dependent on the quality of your sensory apparatus. Once the quantum behaviors of the photons cease to be measurable by your particular apparatus, it is reasonable to declare it is moving as a light wave because you have no way to distinguish the results you see from those predicted by a light wave.
I'm afraid that linear polarization is not as interesting an example as you may have hoped.
First, the answer: in quantum optics, whether or not a quantum state exhibits linear polarization is independent of the photon count for that state. A single-photon state can be linearly polarized.
Now, the explanation: in quantum electrodynamics (QED) it is convenient (especially if you want to perform any actual calculations!) to quantize the field in terms of circularly polarized quanta we usually call photons. However, so long as you are only interested in the electromagnetic field ("quantum optics") it is equally valid [see footnote] - and in this case a better choice - to quantize in terms of linearly polarized quanta. (When I was studying quantum optics, we usually called these photons too, though I'm not sure whether that is considered technically correct or not.)
Specifically, in a thought experiment about a one-dimensional cavity with an ideal linearly polarizing filter part way along, the most natural quanta divide into three groups: those with the linear polarization that the filter passes through, those on the left of the filter with the linear polarization that the filter reflects, and those on the right of the filter with the linear polarization that the filter reflects.
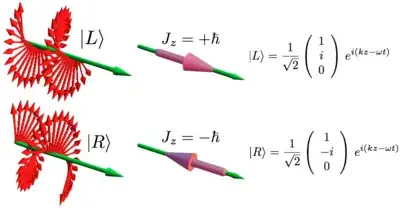
There's nothing mysterious about this, because translating between a state described in terms of linearly polarized quanta and a state described in terms of circularly polarized quanta is trivial. If I remember correctly, in open space (or a simple cavity) a state containing exactly one linearly polarized quanta is just an equal superposition of the state containing a single photon with right circular polarization and the state containing a single photon with left circular polarization. (The orientation of the linear polarization is determined by the phase between the two component states.)
In an actual experiment, of course, you would not expect to see classical polarization at very low (single photon) intensities, because we don't have any ideal polarizing filters to experiment on. However, the photon count necessary to make the experiment work would depend not on the nature of light but on the exact mechanics of the polarizing filter itself.
PS: I am not familiar enough with QED to be absolutely certain, but as far as I know it is still true that you could in principle work with linearly polarized quanta, it just isn't a useful choice if you want to perform any actual calculations.
