What is the use of a Universal-NOT gate?

Question

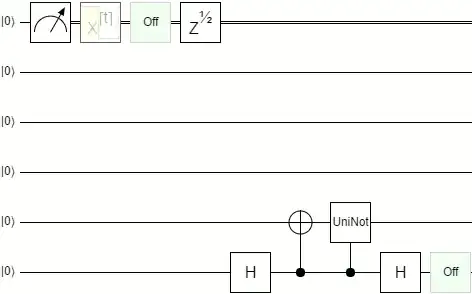
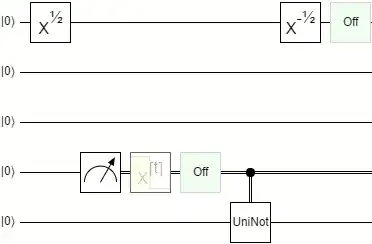
The universal-NOT gate in quantum computing is an operation which maps every point on the Bloch sphere to its antipodal point (see Buzek et al, Phys. Rev. A 60, R2626–R2629). In general, a single qubit quantum state, $|\phi\rangle = \alpha |0\rangle + \beta | 1 \rangle$ will be mapped to $\beta^* |0\rangle - \alpha^*| 1 \rangle$. This operation is not unitary (in fact it is anti-unitary) and so is not something that can be implemented deterministically on a quantum computer.

Optimal approximations to such gates drew quite a lot of interest about 10 years ago (see for example this Nature paper which presents an experimental realization of an optimal approximation).

What has been puzzling me, and what I cannot find in any of the introductions to these papers, is why one would ever want such a gate. Is it actually useful for anything? Moreover, why would one want an approximation, when there are other representations of $SU(2)$ for which there is a unitary operator which anti-commutes with all of the generators?

This question may seem vague, but I believe it has a concrete answer. There presumable is one or more strong reasons why we might want such an operator, and I am simply not seeing them (or finding them). If anyone could enlighten me, it would be much appreciated.

Answer 1

I can imagine a number of reasons why one may want to realize such a gate.

The first is that the universal-NOT exists in classical theory (it is just flipping). This is similar to the case of cloning, that is possible in classical theory but not in quantum theory. So you can look at the study of an approximate universal-NOT as something similar to the study of an approximate cloner (actually, it is easy to argue that if cloning is possible, then universal-NOT is possible: just clone to identify the state, and then rotate it).

The second reason it that the universal-NOT is related to time reversal, and if we want to simulate the latter, we may want to have the former.

The third reason is that the universal-NOT is related to transposition, and as such could be used to test for the presence of entanglement when applied to part of a larger system (partial transposition test).

You can find more recent results and hopefully some more motivation in http://arxiv.org/abs/1104.3039

Answer 2

A Universal-Not allows FTL communication

I added a Universal-Not gate to my toy circuit simulator and played around with it, trying to find interesting things. I was experimenting with "measuring along the UniversalNot axis" when I stumbled onto this:

The left half of the circuit is only varying the global phase, but by the end an observable is varying. The right half of the circuit sends $|00\rangle$ to $|00\rangle$ but sends $i|00\rangle$ to $i|01\rangle$. The system isn't linear w.r.t. the complex amplitudes anymore; it's like the real and imaginary parts have separated.

Turns out this is pretty useful, since anyone anywhere can affect the global phase. With a few tweaks, we have a controlled-UniversalNot gate performing FTL communication with no prior coordination required!

Here's a circuit that does that:

And here's a construction where the Universal-Not's control doesn't need to be coherent. It can be classical, like a person deciding whether or not to press a button.

Here's that circuit:

There's only one communication channel (the global phase channel). So everyone anywhere in the universe using this would be talking over each other. Not to mention the noise introduced by any electron happening to have its spin rotated. But still.

Note that whether or not the receiver could get the message before it was sent (or at all) would depend on which interpretations of quantum mechanics and relativity are correct. The implementation details of my circuit simulator mean that moving the receiver to a column before the sender results in no-message-sent. Basically a controlled-universal-not allows you to do interesting interpretation-falsifying experiments.

Answer 3

[Edited as my original answer misunderstood the question]

The immediate application I can see is in dynamical decoupling. The pulse sequences needed for that are a modified form of the not operation, projecting the state to a point opposite a given symmetry plane on the Bloch sphere. At the moment, the problem there is that the sequences that have been found correct decoherence along one axis on the Bloch sphere. A universal-NOT would be able to generate a universal dynamical decoupler. In essense, for any system and any type of decoherence, we could "run time backwards" and re-extract a coherent system.

(It is maybe interesting to think that, given the links with the no-cloning theorem, there may well be a connection between no cloning and the appearance of a decoherence arrow of time.)

Answer 4

I suppose, the reason for U-Not gate is more clear in wider framework of research of universal quantum machines, conducted by V. Buzek et. al. So U-Not is coming in good company with question about universal quantum cloning (it is also impossible to do precisely, so it is question about most perfect approximation) and other elementary operations. An introduction to U-Not may be found here http://arxiv.org/abs/quant-ph/9901053 (seems it is just online version of second reference in Nature paper cited above).

Answer 5

A universal NOT gate would allow deterministic remote state preparation with one classical communication bit. See http://arxiv.org/abs/1505.05615 and references.