1

disk

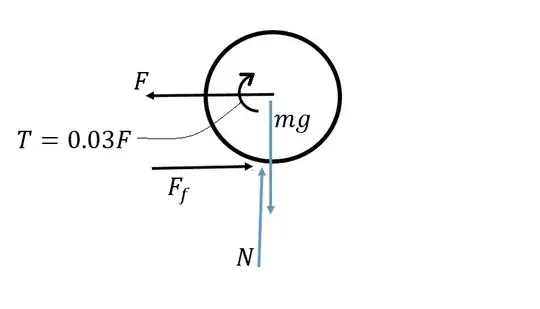
I'm trying to find the friction coefficient that makes the body roll without slipping but I just can't reach a value. The force is applied on a small central disk of radius $r=0,03\, m$ and mass $m=0,05\, kg$. Each big disk has a radius $r=0,05\, m$ and mass $m=0,01\, kg$. That's all the information that is given. My first attempt was to write all the equations that would be useful:

$$F=MA_{cm},\quad T=Ia,\quad V_{cm}=RW.$$

I understand each of the equations but as I substitute $F= 0,1-Fa$ and $T=FaR-0,1r$, I just can't work out the friction force. My question is am I supposed to try the forces approach or the energy approach, since the total energy is conserved? I've tried both approaches but it seems like I am forgetting something. I've been trying to find solutions but most of the problems involve inclined planes, which is different. Thank you very much!

lucas
  • 3,199
George Sailor
  • 79

2 Answers2

1

Transmit the force $F$ to the center of mass and add its torque. Consider to the relative motion between disc and ground. Then you can recognize the correct direction of friction force (friction force opposes relative motion). Free body diagram of disc is as below. (See this answer to understand better.)

enter image description here

Equations of motion are: $$F-F_f=ma$$ $$N=mg$$ $$F_f(0.05)-T=I\alpha$$ $$a=0.05\alpha$$

Community
  • 1
lucas
  • 3,199
1

You say "rolling without slipping." But what do you think will happen in this situation? Do you think the large disk will "roll without slipping"? Can you do an experiment at home to find out?

You can use whatever method gets you to the correct answer. You are given forces (F, weight) so try using forces. Try solving the equations lucas gives you.

UPDATE

Sorry, I have made a mistake here. I was suggesting that it is impossible for the disk to roll without slipping. This is incorrect : it can do so.

I was assuming that F is applied via a string wrapped around the inner disk, and that this string does not slip. In that case it would be impossible for the large disk to move to the left without slipping against the ground, unless the string were wound in the opposite direction so that F is applied above the CM of the disks.

However, there is nothing in the question to say that the string does not slip against the inner disk. Alternatively F could be applied in some other way, not using a string. In this case the outer disk can roll to the left without slipping against the ground.

sammy gerbil
  • 27,586